题目内容
正常水位时,抛物线拱桥下的水面宽为BC=20m,水面上升3m达到该地警戒水位DE时,桥下水面宽为10m.若以BC所在直线为x轴,BC的垂直平分线为y轴,建立如图所示的平面直角坐标系.
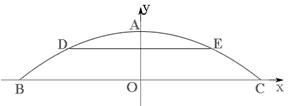
(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?

(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?
(1) 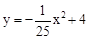 ; (2)5;(3) 能通过,理由见解析.
; (2)5;(3) 能通过,理由见解析.
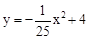 ; (2)5;(3) 能通过,理由见解析.
; (2)5;(3) 能通过,理由见解析.试题分析:(1)依题意得:B(-10,0),C(10,0),D(-5,3),E(5,3),应用待定系数法可得桥孔抛物线的函数关系式;
(2)首先求出警戒水位到桥面的距离,再求出时间t;
(3)求出x=2时的y值与0.75+3比较即可.
试题解析:(1)依题意得:B(-10,0),C(10,0),D(-5,3),E(5,3)
设函数解析式为:y=a(x-10)(x+10),
将 E(5,3)代入,得3=-75a,解得a=
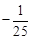 .
.∴桥孔抛物线的函数关系式为y=
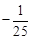 (x-10)(x+10),即
(x-10)(x+10),即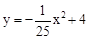 .
.(2)∵t=
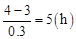 ,∴达到警戒水位后,再过5h此桥孔将被淹没.
,∴达到警戒水位后,再过5h此桥孔将被淹没.(3)若x=2时,
 ,∴能通过.
,∴能通过.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题:
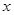 元,此时的销售量是多少?(用含
元,此时的销售量是多少?(用含
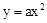 的图象经过点P(2,8),则该图象必经过点
的图象经过点P(2,8),则该图象必经过点 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
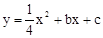 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0,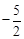 ).直
).直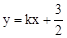 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.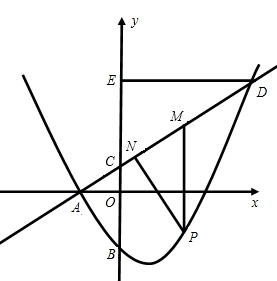
 的图象经过x轴上的二点,它们的坐标分别是:(-4,0),(2,0).当x的取值范围是 时,y随x的增大而减小.
的图象经过x轴上的二点,它们的坐标分别是:(-4,0),(2,0).当x的取值范围是 时,y随x的增大而减小.