题目内容
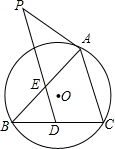
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD.

(1)证明:AF平分∠BAC;
(2)证明:BF=FD.

证明:(1)连接OF.(如图1)
∵FH是⊙O的切线,
∴OF⊥FH.
∵FH∥BC,
∴OF垂直平分BC,
∴
=
,
∴AF平分∠BAC;
(2)∵AF平分∠BAC,
∴∠1=∠2,
∵BD平分∠ABC,
∴∠3=∠4,
又∵∠5=∠2(圆周角定理),
∴∠1+∠4=∠2+∠3,
∴∠1+∠4=∠5+∠3,
∠FDB=∠FBD,
∴BF=FD.

∵FH是⊙O的切线,
∴OF⊥FH.
∵FH∥BC,
∴OF垂直平分BC,
∴
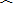 |
| BF |
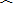 |
| FC |
∴AF平分∠BAC;
(2)∵AF平分∠BAC,
∴∠1=∠2,
∵BD平分∠ABC,
∴∠3=∠4,
又∵∠5=∠2(圆周角定理),
∴∠1+∠4=∠2+∠3,
∴∠1+∠4=∠5+∠3,
∠FDB=∠FBD,
∴BF=FD.


练习册系列答案
相关题目