题目内容
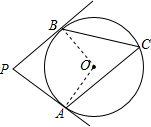
如图，PA、PB是⊙O的切线，切点为A、B，C是⊙O上的一点，已知∠APB=76°，则∠ACB=______．
连接OB、OA、
∵PA、PB是⊙O的切线，切点为A、B，
∴∠PBO=∠PAO=90°，
∵∠APB=76°，
∴∠AOB=360°-∠PBO-∠PAO-∠APB=104°，
∴由圆周角定理得：∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：52°．
练习册系列答案
智能训练练测考系列答案
相关题目
连接OB、OA、
∵PA、PB是⊙O的切线，切点为A、B，
∴∠PBO=∠PAO=90°，
∵∠APB=76°，
∴∠AOB=360°-∠PBO-∠PAO-∠APB=104°，
∴由圆周角定理得：∠ACB=
故答案为：52°．
智能训练练测考系列答案
AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC．
