Question

【题目】在△ABC中，AB=AC，D是BC的中点，以AC为腰向外作等腰直角△ACE，∠EAC=90°，连接BE，交AD于点F，交AC于点G.

(1)若∠BAC=40°，求∠AEB的度数；

(2)求证:∠AEB=∠ACF.

Answer 1

【答案】(1)25°；(2)证明见解析.

【解析】

（1）已知AB=AC，△ACE是等腰直角三角形，可得AB=AE；再由等腰三角形的性质可得∠ABE=∠AEB，由已知条件求出∠BAE的度数，再根据三角形内角和定理即可求出∠AEB的度数；（2）根据等腰三角形的性质得出∠BAF=∠CAF，根据SAS推出△BAF≌△CAF，根据全等得出∠ABF=∠ACF，即可证得结论.

（1） ∵AB=AC，△ACE是等腰直角三角形，

∴AB=AE，

∴∠ABE=∠AEB，

又∵∠BAC=40°，∠EAC=90°，

∴∠BAE=40°+90°=130°，

∴∠AEB=（180°-130°）÷2=25°．

（2）证明：∵AB=AC，D是BC的中点，

∴∠BAF=∠CAF．

在△BAF和△CAF中

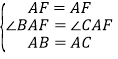
∴△BAF≌△CAF（SAS），

∴∠ABF=∠ACF，

∵∠ABE=∠AEB，

∴∠AEB=∠ACF．