Question

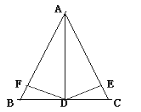
【题目】如图，等边△ABC的边长为3，F为BC边上的动点，FD⊥AB于D，FE⊥AC于E，则DE的长为（ ）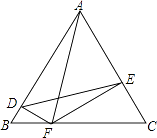

A.随F点运动，其值不变
B.随F点运动而变化，最大值为
C.随F点运动而变化，最小值为
D.随F点运动而变化，最小值为

Answer 1

【答案】D
【解析】解：作AG⊥BC于G，
∵△ABC是等边三角形，
∴∠B=60°，
∴AG= AB= ，
∵S△ABF+S△ACF=S△ABC ，
∴ ABDF+ ACEF= BCAG，
∵AB=AC=BC=2，
∴DF+EF=AG= ，
∵△DEF中，DE＜DF+EF，
∴DE的长随F点运动而变化，最小值为 ．
故选：D．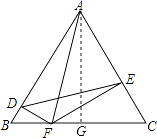

【考点精析】掌握等边三角形的性质和等边三角形的判定是解答本题的根本，需要知道等边三角形的三个角都相等并且每个角都是60°；三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形．