题目内容
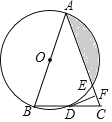
【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
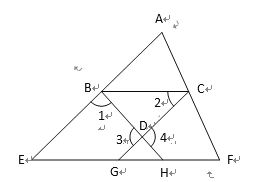
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
【答案】对顶角相等;∠3;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
【解析】
根据对顶角相等,得出∠3=∠4,根据等量代换可知∠1+∠3=180°,根据同旁内角互补,两直线平行,得出AE∥CG,再由两直线平行,同位角相等,得出∠E=∠CGF,已知∠2=∠E,由等量代换可知∠2=∠CGF,再根据内错角相等,两直线平行,即可得出EF∥BC.
证明:∵∠1+∠4﹦180(已知),
∠3﹦∠4 ( 对顶角相等 ),
∴∠1﹢∠3﹦180°.
∴AE∥CG ( 同旁内角互补,两直线平行)
∴∠E﹦∠CGF(两直线平行,同位角相等 ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( 等量代换 ).
∴ BC∥EF(内错角相等,两直线平行).

练习册系列答案
相关题目