题目内容
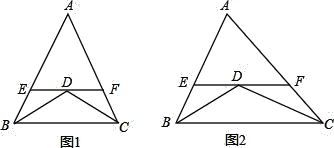
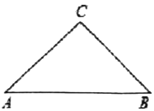
【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

【答案】(1)∠DAE=20°;(2)见解析
【解析】
(1)根据等边对等角和已知∠ABC的度数可求得∠CAE的度数,再根据等腰三角形三线合一的性质可得AD⊥BC,然后根据直角三角形的性质可求出∠DAC的度数,进一步即可求出结果;
(2)先根据等角对等边得到AF=AE,再根据等腰三角形三线合一的性质得FD=ED,进一步即得结论.
解:(1)∵AB=AC,∠ABC=35°,∴∠C=35°,
∵AE=CE,∴∠CAE=∠C=35°,
∵D是BC边上的中点,∴AD⊥BC,∴∠ADC=90°,
∴∠DAC=90°﹣35°=55°,
∴∠DAE=∠DAC﹣∠CAE=55°﹣35°=20°;
(2)证明:∵∠AFE=∠AEF,∴AF=AE,
∵AD⊥BC,∴D是EF边上的中点,∴FD=ED,
∵D是BC边上的中点,∴BD=CD,
∴BD﹣FD=CD﹣ED,即BF=CE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目