Question

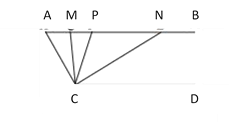
【题目】如图，已知AB∥CD，∠A=40°，点P是射线B上一动点（与点A不重合），CM，CN分别平分∠ACP和∠PCD，分别交射线AB于点M,N．

（1）求∠MCN的度数．

（2）当点P运动到某处时，∠AMC=∠ACN，求此时∠ACM的度数．

（3）在点P运动的过程中，∠APC与∠ANC的比值是否随之变化？若不变，请求出这个比值：若变化，请找出变化规律．

Answer 1

【答案】（1）∠MCN=70°；（2）∠ACM=35°；（3）不变．（详见解析）

【解析】

（1）由AB∥CD可得∠ACD=180°-∠A，再由CM、CN均为角平分线可求解；

（2）由AB∥CD可得∠AMC=∠MCD，再由∠AMC=∠ACN可得∠ACM =∠NCD；

（3）由AB∥CD可得∠APC=∠PCD，再由CN为角平分线即可解答．

解：（1）∵A B∥CD，

∴∠ACD=180°﹣∠A=140°，

又∵CM，CN分别平分∠ACP和∠PCD，

∴∠MCN=∠MCP+∠NCP=（∠ACP+∠PCD）=∠ACD=70°，

故答案为：70°．

（2）∵AB∥CD，

∴∠AMC=∠MCD，

又∵∠AMC=∠ACN，

∴∠MCD=∠ACN，

∴∠ACM=∠ACN﹣∠MCN=∠MCD﹣∠MCN=∠NCD，

∴∠ACM=∠MCP=∠NCP=∠NCD，

∴∠ACM=∠ACD=35°，

故答案为：35°．

（3）不变．理由如下：

∵AB∥CD，

∴∠APC=∠PCD，∠ANC=∠NCD，

又∵CN平分∠PCD，

∴∠ANC=∠NCD=∠PCD=∠APC，即∠APC：∠ANC=2：1．