题目内容
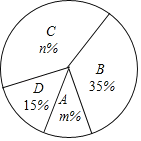
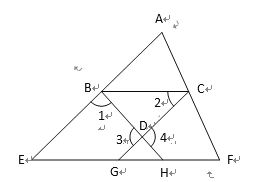
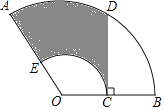
【题目】如图，扇形OAB中，∠AOB=100°，OA=12，C是OB的中点，CD⊥OB交
于点D，以OC为半径的
交OA于点E，则图中阴影部分的面积是（ ）
A. 12π+18
B. 12π+36 C. 6π+18 D. 6π+36
【答案】C
【解析】
连接OD、AD，根据点C为OA的中点可得∠CDO=30°，继而可得△ADO为等边三角形，求出扇形AOD的面积，最后用扇形AOB的面积减去扇形COE的面积，再减去S空白ADC即可求出阴影部分的面积．
如图，连接OD，BD，
∵点C为OB的中点，
∴OC=
OB=OD，
∵CD⊥OB，
∴∠CDO=30°，∠DOC=60°，
∴△BDO为等边三角形，OD=OB=12，OC=CB=6，
∴CD=6
，
∴S扇形BOD=
=24π，
∴S阴影=S扇形AOB﹣S扇形COE﹣（S扇形BOD﹣S△COD）
=
=18+6π，
故选C．
练习册系列答案
阅读快车系列答案
相关题目
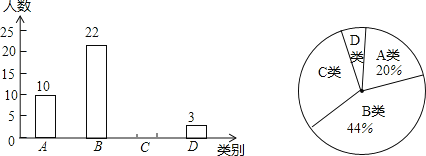
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
