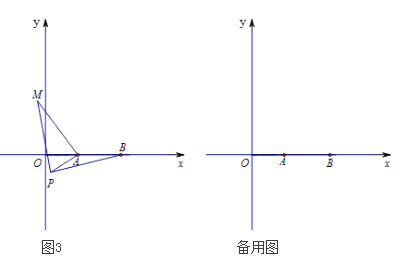
题目内容
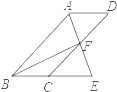
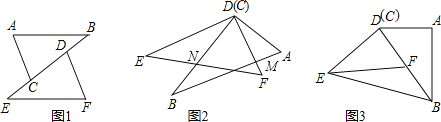
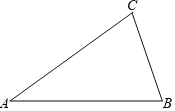
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A’B’C’,若它移动的距离AA’等于1cm,则两个三角形重叠部分的面积为____________cm2.
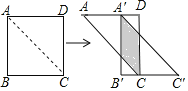
【答案】1
【解析】
设AC与A′B′交于点E,A′C′与DC交于点F,由正方形的性质得到△ACD和△A′B′C′都为直角边为2cm的等腰直角三角形;从而判定出△AA′E也为等腰直角三角形,得到A′E=AA′=1cm,从而得到A′D的长;由正方形的性质与三角形的面积公式即可求出两三角形重叠的面积.
对图形进行点标注,
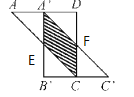
∵ 四边形ABCD是正方形边长为2cm,
∴ ∠ADC=90° ,AD=DC=2cm,∠DAC=45°,
∵△ A′ B′C′是由△ABC沿着AD方向平移得到的,
∴ AC∥A′C′,∠EA′A=90°,
∵ ∠DAC=45°,∠EA′A=90°,
∴△EAA′是等腰直角三角形,
∵AA′=1cm,△EAA′是等腰直角三角形,
∴![]()
∵ AC∥A′C′,∠DAC=45°,
∴ ∠FA′D=45°,
∵∠DA′F=45°,∠ADC=90°,
∴△FDA′是等腰直角三角形,
∵ AD=2cm,AA′=1cm,
∴A′D=1cm,
∵△FDA′是等腰直角三角形,A′D=1cm,
![]()
同理可得到![]() (cm2),
(cm2),
∴S阴影=![]() (cm2).
(cm2).
故答案为:1.

练习册系列答案
相关题目