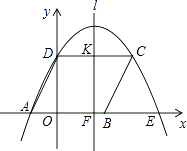Question

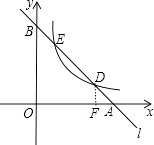
【题目】如图，已知直线l分别与x轴、y轴交于A，B两点，与双曲线y= （a≠0，x＞0）分别交于D、E两点．

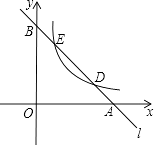
（1）若点D的坐标为（4，1），点E的坐标为（1，4）：
①分别求出直线l与双曲线的解析式；
②若将直线l向下平移m（m＞0）个单位，当m为何值时，直线l与双曲线有且只有一个交点？
（2）假设点A的坐标为（a，0），点B的坐标为（0，b），点D为线段AB的n等分点，请直接写出b的值．

Answer 1

【答案】
（1）

解：①把D（4，1）代入y= 得a=1×4=4，

所以反比例函数解析式为y= （x＞0）；

设直线l的解析式为y=kx+t，

把D（4，1），E（1，4）代入得 ，

解得 ．

所以直线l的解析式为y=﹣x+5；

②直线l向下平移m（m＞0）个单位得到y=﹣x+5﹣m，

当方程组 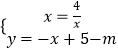只有一组解时，直线l与双曲线有且只有一个交点，

化为关于x的方程得x2+（m﹣5）x+4=0，

△=（m﹣5）2﹣4×4=0，解得m1=1，m2=9，

而m=9时，解得x=﹣2，故舍去，

所以当m=1时，直线l与双曲线有且只有一个交点

（2）

解：作DF⊥x轴，如图，

∵点D为线段AB的n等分点，

∴DA：AB=1：n，

∵DF∥OB，

∴△ADF∽△ABO，

∴ ，即 ，

∴AF= ，DF= ，

∴OF=a﹣ ，

∴D点坐标为（a﹣ ， ），

把D（a﹣ ， ）代入y= 得（a﹣ ） =a，

解得b= ．

【解析】（1）①运用待定系数法可分别得到直线l与双曲线的解析式；
②直线l向下平移m（m＞0）个单位得到y=﹣x=5﹣m，根据题意得方程组 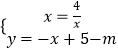只有一组解时，化为关于x的方程得x2+（m﹣5）x+4=0，则△=（m﹣5）2﹣4×4=0，解得m1=1，m2=9，当m=9时，公共点不在第一象限，所以m=1；（2）作DF⊥x轴，由DF∥OB得到△ADF∽△ABO，根据相似比可得到AF= ，DF= ，则D点坐标为（a﹣ ， ），然后把D点坐标代入反比例函数解析式中即可得到b的值．
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点，需要掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能正确解答此题．