��Ŀ����
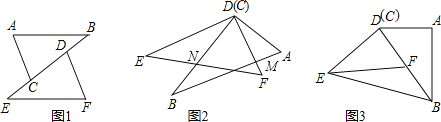
����Ŀ����ͼ1��ʾ����֪�ڡ�ABC�͡�DEF�У�AB=EF����B=��E��EC=BD
��1����˵������ABC�ա�FED��
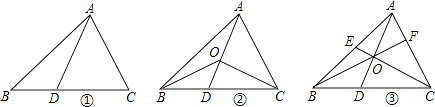
��2����ͼ�ξ���ƽ�ƺ���ת��õ�ͼ2�����С�EDB=25�㣬��A=66�㣬�����AMD�Ķ�����
��3����ͼ�μ�����ת��õ�ͼ3����ʱD��B��F������ͬһ��ֱ���ϣ���DB=2DF������EB����֪��EFB�����Ϊ5cm2����������ı���ABED����������ܣ���������������ܣ�����˵�����ɣ�
���𰸡�������
��������
���⣨1����EC=BD����ʽ�������߶�����DC���õ�ED=BC��������B=��E��AB=EF������SAS��֤��������ABC��������FEDȫ�ȣ�
��2����������ABC��������FEDȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ��õ���EDF=��BDA���Ⱥ����߶���ȥ��BDF���õ���EDB=��ADF������EDB�Ķ����õ���ADF�Ķ�������������AMD�У�����ADF����A�Ķ��������������ε��ڽǺͶ������������AMD�Ķ�����
��3����BD=2DF���õ�ΪDB���е㣬�ɵ�DF=BF�����õȵ�ͬ�߿ɵ�������DEF��������EFB�����ȣ���������ABD��������DEFȫ�ȣ��õ�������ABD��������DEF�����ȣ��ɵ�������DEF��������EFB��������ABD���������ȣ���������EFB������ɵó������������ε������������ӿɵó��ı���ABED�������
�����������1����EC=BD����֪����
��EC+CD=BD+DC����ED=BC��
����ABC����FED��
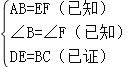 ��
��
���ABC�ա�FED��SAS����
��2���ߡ�ABC�ա�FED��
���EDF=��BDA��
���EDF����BDF=��BDA����BDF������EDB=25����
���EDB=��ADF=25��������A=66����
���AMD=180�㩁66�㩁25��=89����
��3��������ı���ABED�����������Ϊ��
�ߡ�ABC�ա�FED��
��S��ABC=S��FED��
��DB=2DF����FΪBD�е㣬
��DF=BF����S��EFB=5��
��S��EDF=S��EFB=S��ABC=5��
��SABCD=S��EDF+S��EFB+S��ABC=15��