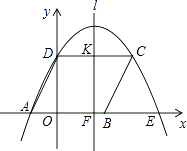��Ŀ����
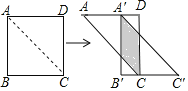
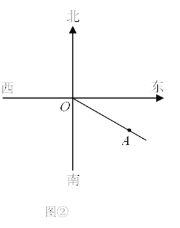
����Ŀ����1����ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b����գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� �����ú�a��b��ʽ�ӱ�ʾ����
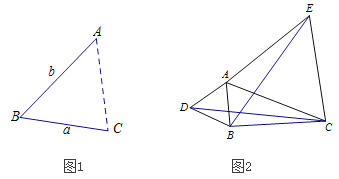
��2����ͼ2������AΪ�߶�BC��һ���㣬��BC=4��AB=2���ֱ���AB��ACΪ�ߣ����ȱ�![]() �͵ȱ�
�͵ȱ�![]() ������CD��BE.
������CD��BE.
��ͼ�����߶�BE��ȵ��߶����߶� ����˵�����ɣ�
��ֱ��д���߶�BE�������ֵΪ ��
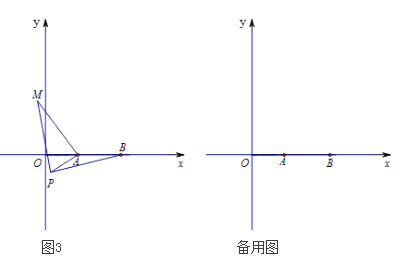
��3����ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA=2��PM=PB����BPM=90�㣬��ֱ��д���߶�AM�������ֵΪ ������ʱ��P������Ϊ ������ʾ������ֱ�������ε����߳�a��b��c����a��b��c=1��1��![]() ��
��
���𰸡���1��CB�ӳ�������a+b��2����DC��6����3��3+2![]() ����2-
����2-![]() ��
��![]() ����2-
����2-![]() ��-
��-![]() ��.
��.
��������
1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ����ۣ�
��2�������ݵȱ������ε����ʵõ�AD=AB��AC=AE����BAD=��CAE=60�����Ƴ���CAD�ա�EAB������ȫ�������ε����ʵõ�CD=BE���������߶�BE�������ֵ=�߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ������
��3������BM������APM���ŵ�P˳ʱ����ת90���õ���PBN������AN���õ���APN�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�PN=PA��BN=AM�����ݵ�N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ�����ɵõ����ֵΪ��P��PE��x����E�����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
��1��CB�ӳ�������a+b��
��2����DC��
�������£��ߡ�ABD���ACE�ǵȱ������Σ�
��AD=AB��AC=AE����BAD=��CAE=60�㣬
���BAD+��BAC=��CAE+��BAC��
����CAD=��EAB��
�ڡ�CAD���EAB�У�
 ��
��
���CAD�ա�EAB��
��CD=BE.
��6
��3��![]()
��2-![]() ��
��![]() ����2-
����2-![]() ��-
��-![]() ��
��

����Ŀ��ij���е�������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������
����ʱ�� | ������ | �������� | |
A�ͺ� | B�ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
��1����A��B�����ͺŵĵ���ȵ����ۼۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ����30̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£�������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ����������ɹ������������ܣ���˵�����ɣ�