题目内容
如图，在同心圆中，大圆的弦AB与小圆相交于点C，D，且AC=CD=DB，若两圆的半径分别为4cm和2cm，则CD的长等于（ ）
| A．3cm | B．2.5cm | C．
| D．
|
如图：
过点O作OE⊥AB于点E，则：AE=BE，CE=DE．
∵AC=CD=DB，
∴AC=2CE．
连接OA，OC，
设CE=a，则AC=2a，AE=3a．
在两个直角三角形中用勾股定理得到：
OE2=OA2-AE2=OC2-CE2
即：16-9a2=4-a2
解得：a=
（-
舍去）
∴CD=2CE=2a=
．
故选D．
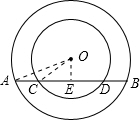
过点O作OE⊥AB于点E，则：AE=BE，CE=DE．
∵AC=CD=DB，
∴AC=2CE．
连接OA，OC，
设CE=a，则AC=2a，AE=3a．
在两个直角三角形中用勾股定理得到：
OE2=OA2-AE2=OC2-CE2
即：16-9a2=4-a2
解得：a=
| ||
| 2 |
| ||
| 2 |
∴CD=2CE=2a=
| 6 |
故选D．
练习册系列答案
全优点练单元计划系列答案
相关题目
