题目内容
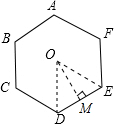
若正六边形的边长等于4，则它的面积等于（ ）
A．48
| B．24
| C．12
| D．4
|
连接正六变形的中心O和两个顶点D、E，得到△ODE，
∵∠DOE=360°×
=60°，
又∵OD=OE，
∴∠ODE=∠OED=（180°-60°）÷2=60°，
则△ODE为正三角形，
∴OD=OE=DE=4，
∴S△ODE=
OD•OM=
OD•OE•sin60°=
×4×4×
=4
．
正六边形的面积为6×4
=24
．
故选：B．
∵∠DOE=360°×
| 1 |
| 6 |
又∵OD=OE，
∴∠ODE=∠OED=（180°-60°）÷2=60°，
则△ODE为正三角形，
∴OD=OE=DE=4，
∴S△ODE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
正六边形的面积为6×4
| 3 |
| 3 |
故选：B．
练习册系列答案
天天向上口算本系列答案
相关题目
