Question

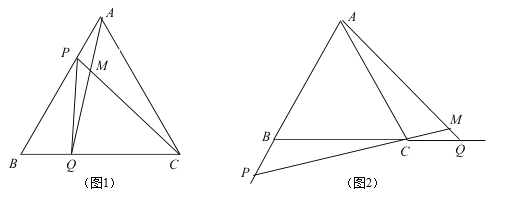
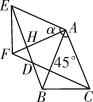
【题目】如图，在△ABC中，AB＝AC＝2，∠BAC＝45°，将△ABC绕点A按顺时针方向旋转角α得到△AEF，且0°＜α≤180°，连接BE，CF相交于点D.

(1)求证：BE＝CF；

(2)当α＝90°时，求四边形AEDC的面积．

Answer 1

【答案】（1）证明见解析；（2）2．

【解析】

（1）先利用旋转的性质得AE＝AB，AF＝AC，∠EAF＝∠BAC，则根据“SAS”证明△AEB≌△AFC，于是得到BE＝CF；
（2）先判断△ABE为等腰直角三角形得到∠ABE＝45°，则AC∥BE，同理可得AE∥CF，于是可证明四边形AEDC为菱形，AF与BE交于点H，如图，通过证明△AHE为等腰直角三角形得到AH＝AE＝，然后根据菱形的面积公式计算．

（1）证明：∵将△ABC绕点A按顺时针方向旋转角α得到△AEF，

∴AE＝AB，AF＝AC，∠EAF＝∠BAC，

∴AB＝AC＝AE＝AF，∠EAF＋∠FAB＝∠BAC＋∠FAB，即∠EAB＝∠FAC.

在△AEB和△AFC中，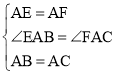

∴△AEB≌△AFC(SAS)，

∴BE＝CF．

（2）解：∵α＝90°，

∴∠EAB＝∠FAC＝90°.

∵AE＝AB，

∴△ABE为等腰直角三角形，

∴∠ABE＝45°，

∴∠ABE＝∠BAC，

∴AC∥BE，

同理可得AE∥CF.

∵AE＝AC，

∴四边形AEDC为菱形．

设AF与BE交于点H.

∵∠EAF＝45°，

∴AH平分∠EAB，

∴AH⊥BE，

∴△AHE为等腰直角三角形，

∴AH＝AE·sin45°AE＝，

∴四边形AEDC的面积为AH·DE＝×2＝2．