题目内容
【题目】综合与探究
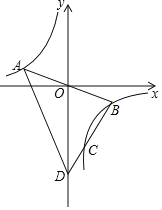
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,其对称轴与抛物线交于点
,其对称轴与抛物线交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 为抛物线对称轴上的一个动点,从点
为抛物线对称轴上的一个动点,从点![]() 出发,沿射线
出发,沿射线![]() 以每秒2个单位长度的速度运动,过点
以每秒2个单位长度的速度运动,过点![]() 作
作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边).设点
的左边).设点![]() 的运动时间为
的运动时间为![]() .
.
①当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
②连接![]() ,在点
,在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标:若不存在,请说明理由;
的坐标:若不存在,请说明理由;
③点![]() 在
在![]() 轴上,点
轴上,点![]() 为坐标平面内一点,以线段
为坐标平面内一点,以线段![]() 为对角线作菱形
为对角线作菱形![]() ,当
,当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①当
;(2)①当![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;②点
为顶点的四边形是平行四边形;②点![]() 从的坐标为
从的坐标为![]() 或
或![]() ;③
;③![]() 或
或![]() .
.
【解析】
(1)利用二次函数图象上点的坐标特征可求出点A,B的坐标,利用配方法可求出抛物线顶点D的坐标;
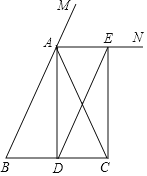
(2)①由MN∥AB可得出当MN=AE时四边形MNEA为平行四边形,由点A,E的坐标结合二次函数的对称性可得出点M的横坐标,利用二次函数图象上点的坐标特征可得出点M的坐标,结合点G的运动方向及速度,即可求出t值;
②过点M作MH⊥x轴,垂足为点H,设点M的坐标为(m,-![]() m2+2m+6)(m<2),则BH=6-m,MH=|-
m2+2m+6)(m<2),则BH=6-m,MH=|-![]() m2+2m+6|,由∠MBA=∠EDB结合正切的定义,可得出关于m的方程,解之即可得出m的值,将其代入点M的坐标即可得出结论;
m2+2m+6|,由∠MBA=∠EDB结合正切的定义,可得出关于m的方程,解之即可得出m的值,将其代入点M的坐标即可得出结论;
③设点M的坐标为(n,-![]() n2+2n+6)(n<2)时PQ=
n2+2n+6)(n<2)时PQ=![]() MN,结合题意可得出关于n的方程,解之即可得出n的值,将其代入点M的坐标可求出点M的坐标,再点G的运动方向及速度,即可求出t值.
MN,结合题意可得出关于n的方程,解之即可得出n的值,将其代入点M的坐标可求出点M的坐标,再点G的运动方向及速度,即可求出t值.
解:(1)当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
点![]() 在点
在点![]() 的左侧,则
的左侧,则![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
(2)①∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,
为顶点的四边形是平行四边形时,![]() ,
,![]() .
.
∵点![]() ,
,![]() 关于对称轴对称,∴
关于对称轴对称,∴![]() .
.
∴点![]() 与点
与点![]() 重合.∴
重合.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴当![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
②∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,即
,即![]() .
.
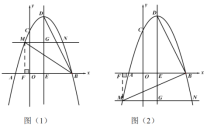
如图(1),当点![]() 在
在![]() 轴上方时,
轴上方时,![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
当![]() 时,
时,![]() ∴
∴![]() .
.
如图(2),当点![]() 在
在![]() 轴下方时,
轴下方时,![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
当![]() 时,
时,![]() .∴
.∴![]() .
.
综上所述,点![]() 从的坐标为
从的坐标为![]() 或
或![]() .
.
③![]() 或
或![]()
解析:点![]() 在
在![]() 轴上,四边形
轴上,四边形![]() 是菱形,
是菱形,
∴点![]() 与点
与点![]() 重合,即
重合,即![]() ,菱形对角线的交点为点
,菱形对角线的交点为点![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
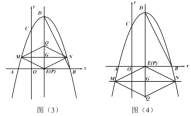
如图(3),当![]() 在
在![]() 轴上方时,
轴上方时,![]() .
.
∵点![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]()
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() .
.
∴![]() .
.
∴![]() .
.
如图(4),当![]() 在
在![]() 轴下方时,
轴下方时,![]() .
.
∵点![]() 在
在![]() 的图象上,
的图象上,
∴![]() .
.
∴![]() .
.
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() .
.
∴![]() .
.
∴![]() .
.
综上所述,![]() 或
或![]()

【题目】在5月31日世界禁烟日到来之际,某校为了提高禁烟意识,在七、八年级举办了“关爱健康,远离香烟”的知识竞赛,两个年级分别有500人为了了解本次竞赛成绩情况,现从中各随机抽取了部分同学的测试成绩x(得分均为整数,满分为100分)进行调查分析,过程如下:
第一步:收集数据
七年级:68 88 100 100 79 94 89 85 100 88 81 69 98 79 77 94 96 75 92 67
八年级:69 97 78 89 98 100 99 100 95 99 99 69 75 100 99 78 79 87 85 79
第二步:整理、描述数据
分数段 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
七年级人数 | 3 | 4 | 5 | 8 |
八年级人数 | 2 | 5 | 3 | 10 |
第三步:分析数据
年级 | 平均数 | 中位数 | 众数 | 满分率 | 方差 |
七年级 | 86 | 88 | 100 | 15% | 115.6 |
八年级 | 88.7 | 92 | a | 15% | 120 |
第四步:应用数据
(1)直接写出a的值和八年级抽取了多少个同学的成绩进行分析
(2)在此次测试中,七年级甲学生的成绩为89分,八年级乙学生成绩为90分,甲、乙两人的成绩在各自年级中哪一个更靠前?请说明理由.
(3)若成绩在90分至99分之间(含90分,99分)的学生为二等奖,请估计七、八年级一共获得二等奖的学生总人数.