题目内容
【题目】下面是小明设计的“作一个以已知线段为对角线正方形”的尺规作图过程.
已知:线段AC
求证:四边形ABCD为正方形
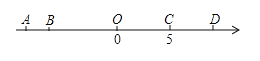
作法:如图,
①作线段AC的垂直平分线MN 交AC于点O;
②以点O为圆心CO长为半径画圆,交直线MN于点B,D;
③顺次连接AB,BC,CD,DA;
所以四边形ABCD为所作正方形.

根据小明设计的尺规作图过程,完成以下任务.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OA=OB,OC=OD,
∴四边形 ABCD为平行四边形.(__________________)(填写推理依据)
∵OA=OB=OC=OD即AC=BD.
∴![]() ABCD为 (__________________)(填写推理依据).
ABCD为 (__________________)(填写推理依据).
∵ AC⊥BD,
∴四边形 ABCD为正方形(__________________________).(填写推理依据)
【答案】对角线互相平分的四边形是平行四边形,矩形,对角线相等且互相平分的四边形是矩形
【解析】
(1)根据作图步骤画出图形即可;
(2)根据对角线相等且互相平分的四边形是矩形进行判定即可.
(1)作图如下;

(2)证明:∵OA=OB,OC=OD,
∴四边形 ABCD为平行四边形.(__对角线互相平分的四边形是平行四边形__)
∵OA=OB=OC=OD即AC=BD.
∴![]() ABCD为 矩形 (__对角线相等且互相平分的四边形是矩形__)(填写推理依据).
ABCD为 矩形 (__对角线相等且互相平分的四边形是矩形__)(填写推理依据).
∵ AC⊥BD,
∴四边形 ABCD为正方形(___对角线互相垂直的矩形是正方形___).(填写推理依据)
故答案为:对角线互相平分的四边形是平行四边形;矩形;对角线相等且互相平分的四边形是矩形;对角线互相垂直的矩形是正方形.

【题目】为了促进学生体育锻炼,某校八年级进行了体育测试,为了解女生体育测试情况,从中抽取了若干名女生的体育测试成绩.
a.体育委员小李在整理频数分布表时,不小心污染了统计表:
分组(分) | 频数 | 频数 |
21<x≤22 | 8 | 0.200 |
22<x≤23 | 4 | n |
23<x≤24 | 7 | 0.175 |
24<x≤25 | 3 | 0.075 |
25<x≤26 | 2 | 0.050 |
26<x≤27 | 8 | 0.200 |
27<x≤28 | m | 0.150 |
28<x≤29 | 2 | 0.050 |
合计 |
|
b.根据频数分布表,绘制如下频数分布直方图:
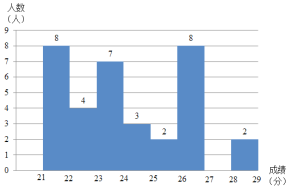
c.在此次测试中,共测试了800米,篮球,仰卧起坐,成绩统计如下:
项目 | 平均分 | 中位数 | 众数 |
800米 | 8.27 | 8.5 | 8.5 |
仰卧起坐 | 7.61 | 8 | 7.5 |
篮球 | 8.69 | 9 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m,n的值;
(2)补全直方图;
(3)请结合C中统计图表,给该校女生体育训练提供建议(至少从两个不同的角度分析).