题目内容
【题目】如图，已知等腰Rt△ABC中，AB=AC，∠BAC=
，点A、B分别在x轴和y轴上，点C的坐标为（6，2）.
（1）如图1，求A点坐标；
（2）如图2，延长CA至点D，使得AD=AC，连接BD，线段BD交x轴于点E，问：在x轴上是否存在点M，使得△BDM的面积等于△ABO的面积，若存在，求点M的坐标；若不存在，请说明理由.
【答案】（1）A（2,0）；（2）（0 ，0）（- 
，0）.
【解析】
（1）过C作CH⊥x轴于H，则CH=2,根据题意可证△ADB≌△CAH，所以OA=CH，又因点A在x轴上，所以点A的坐标为（2,0）.
（2）根据题意先求出点D的坐标为（2，-2），再根据△BDM的面积=△BEM的面积+△DEM的面积=△ABO的面积，列出方程解出M点的坐标.
（1）过C作CH⊥x轴于H，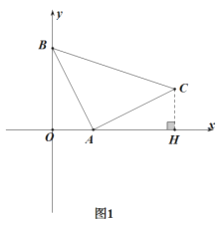
则△ADB≌△CAH，
又C（6,2），
所以，OA＝2，即A（2,0）
（2）如图2所示，设点M的坐标为（x，0），
∵AD=AC,
∴点A是CD的中点，
∵C（6,2），A（2，0）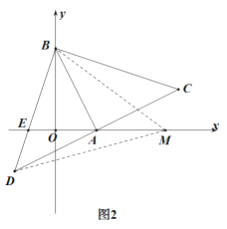
∴D（-2，-2）.
设直线BD的解析式为y=kx+b,则
解得：
∴直线BD的解析式为
，
令y=0，解得x=
.
∴E的坐标为（，0）
∵△BDM的面积=△BEM的面积+△DEM的面积=△ABO的面积
∴
解得：
或x=0.
∴点M的坐标（0 ，0）或（- ，0）..
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示：
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利（元） | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜，已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨（两种加工不能同时进行）。
（1）如果要求在18天内全部销售这140吨蔬菜，请完成下列表格：
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工，剩余部分直接销售 |
获利（元） |
（2）如果先进行精加工，来不及精加工的进行粗加工，要求15天内刚好加工完这140吨蔬菜，则应如何分配加工时间？
