题目内容
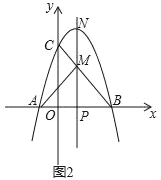
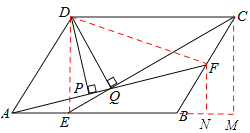
【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
【答案】D
【解析】
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
∵根据三角形的面积和平行四边形的面积得:
![]() ,即
,即![]() 。
。
∴AF×DP=CE×DQ,。
∵四边形ABCD是平行四边形,∴AD∥BC。
∵∠DAB=60°,∴∠CBN=∠DAB=60°。∴∠BFN=∠MCB=30°。
∵AB:BC=3:2,∴设AB=3a,BC=2a。
∵AE:EB=1:2,F是BC的中点,∴BF=a,BE=2a,BN=![]() a,BM=a。
a,BM=a。
由勾股定理得:FN=![]() a,CM=
a,CM=![]() a。
a。
∴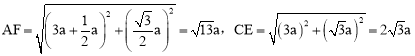 。
。
∴![]() 。∴
。∴![]() 。故选D。
。故选D。

练习册系列答案
相关题目
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,来不及精加工的进行粗加工,要求15天内刚好加工完这140吨蔬菜,则应如何分配加工时间?