Question

【题目】如图，在△ABC中，∠C=60°，∠A=40°．

（1）用尺规作图作AB的垂直平分线，交AC于点D，交AB于点E（保留作图痕迹，不要求写作法和证明）；
（2）求证：BD平分∠CBA．

Answer 1

【答案】
（1）

解：如图1所示：

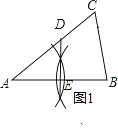
（2）

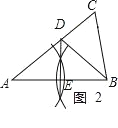
证明：连接BD，如图2所示：

∵∠C=60°，∠A=40°，

∴∠CBA=80°，

∵DE是AB的垂直平分线，

∴∠A=∠DBA=40°，

∴∠DBA=∠CBA，

∴BD平分∠CBA．

【解析】（1）分别以A、B两点为圆心，以大于AB长度为半径画弧，在AB两边分别相交于两点，然后过这两点作直线即为AB的垂直平分线；
（2）根据线段垂直平分线的性质和三角形的内角和证明即可．
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．