题目内容
【题目】定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.
(1)max{![]() ,3}= ;
,3}= ;
(2)已知y1=![]() 和y2=k2x+b在同一坐标系中的图象如图所示,若max{
和y2=k2x+b在同一坐标系中的图象如图所示,若max{![]() ,k2x+b}=
,k2x+b}=![]() ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;
(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.
【答案】
(1)3
(2)
∵max{![]() ,k2x+b}=
,k2x+b}=![]() ,
,
∴![]() ≥k2x+b,
≥k2x+b,
∴从图象可知:x的取值范围为﹣3≤x<0或x≥2;
(3)
当2x+1≥x﹣2,即x![]() -3时,max{2x+1,x﹣2}=2x+1,
-3时,max{2x+1,x﹣2}=2x+1,
当2x+1<x﹣2,即x<-3时,max{2x+1,x﹣2}=x﹣2.
【解析】(1)根据3>![]() 和已知求出即可;
和已知求出即可;
(2)根据题意得出![]() ≥k2x+b,结合图象求出即可;
≥k2x+b,结合图象求出即可;
(3)分为两种情况:当2x+1≥x﹣2时,当2x+1<x﹣2时,结合已知求出即可.

【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表: 该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题: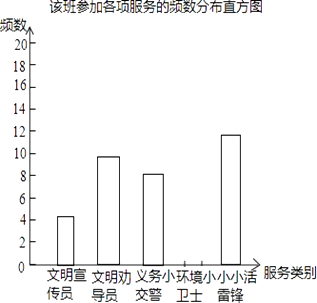
(1)该班参加这次公益活动的学生共有名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.




