��Ŀ����
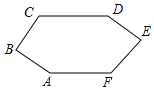
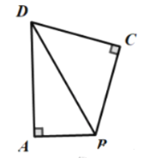
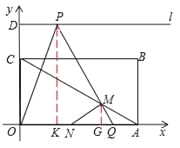
����Ŀ����ͼ������OABC�У�A��6��0����C��0��2![]() ����D��0��3
����D��0��3![]() ��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬������PQO=60����
��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬������PQO=60����
��1������B���������� �����ڡ�CAO=�� ���ȣ�������Q���A�غ� ʱ����P������Ϊ�� ������ֱ��д���𰸣�
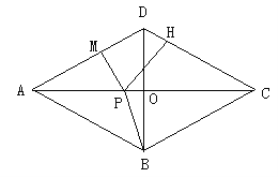
��2����OA���е�ΪN��PQ���߶�AC�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ��AMNΪ���������Σ������ڣ���ֱ��д����P�ĺ�����Ϊm���������ڣ���˵�����ɣ�
��3�����P�ĺ�����Ϊx����OPQ�����OABC���ص����ֵ����ΪS������S��x�ĺ�����ϵʽ����Ӧ���Ա���x��ȡֵ��Χ��

���𰸡���1������6��2![]() ������30������3��3
������30������3��3![]() ����(2)m=0��m=3��
����(2)m=0��m=3��![]() ��m=2����3����0��x��3ʱ��S����=
��m=2����3����0��x��3ʱ��S����=![]() ��3+x������3��x��5ʱ��S=
��3+x������3��x��5ʱ��S=![]() ��3+x����
��3+x����![]() ��x��3��2����5��x��9ʱ��S=
��x��3��2����5��x��9ʱ��S=![]() ��12��
��12��![]() x������9��xʱ��S=
x������9��xʱ��S=![]() ��
��
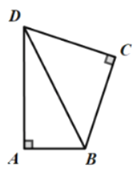
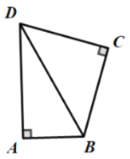
�����������ε����ʣ����ε����ʣ�������Ǻ���������ǵ����Ǻ���ֵ�����������ε��ж������ʣ���ֱ�������Ρ�
��1�������ı���OABC�Ǿ��Σ����ݾ��ε����ʣ�������õ�B�����꣺
���ı���OABC�Ǿ��Σ���AB=OC��OA=BC��
��A��6��0����C��0��2![]() ��������B����������6��2
��������B����������6��2![]() ����
����
�������к��������������CAO�Ķ�����
��![]() �����CAO=30����
�����CAO=30����
�������Ǻ��������ʣ�������õ�P�����ꣻ��ͼ������Q���A�غ�ʱ������P��PE��OA��E��
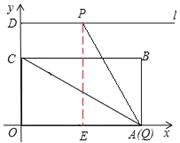
�ߡ�PQO=60����D��0��3![]() ������PE=3
������PE=3![]() ��
��
��![]() ��
��
��OE=OA��AE=6��3=3������P��������3��3![]() ����
����
��2���ֱ��MN=AN��AM=AN��AM=MNȥ������⼴����ô𰸣�
�������
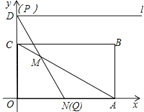
MN=AN=3������AMN=��MAN=30����
���MNO=60����
�ߡ�PQO=60��������MQO=60��������N��Q�غϡ�
����P��D�غϡ�����ʱm=0��
���������ͼAM=AN����MJ��x�ᡢPI��x�ᡣ
MJ=MQsin60��=AQsin600
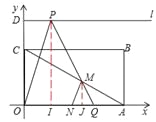
![]()
��![]() ��
��
��![]() ����ã�m=3��
����ã�m=3��![]() ��
��
�����AM=NM����ʱM�ĺ�������4.5��
����P��PK��OA��K������M��MG��OA��G��
��MG=![]() ��
��
��![]() ��
��
��KG=3��0.5=2.5��AG=![]() AN=1.5����OK=2����m=2��
AN=1.5����OK=2����m=2��
������������P�ĺ�����Ϊm=0��m=3��![]() ��m=2��
��m=2��
��3���ֱ�ӵ�0��x��3ʱ����3��x��5ʱ����5��x��9ʱ����x��9ʱȥ������⼴����ô𰸡�

����Ŀ��ij������2007����Ͷ��һ���ʽ�Ӵ���������ĸ������ȣ����ֲ�Ӱ��Խ��������������Ͷ�룮�������й滮�ֵȲ����ṩ����Ϣ��
2002�� | 2003�� | 2004�� | 2005�� | |
���������ʽ� | 1.2 | 1.4 | 1.5 | 1.6 |
���������ʽ� | 5.8 | 6.1 | 6.25 | 6.4 |
��2007������������������ʽ���2007�����Ͷ���3����
�ڼƻ�2007���2006��Ľ���Ͷ���0.5��Ԫ����������Ľ���Ͷ��֮��Ϊ6��5��
������������������ʽ�һ����������������������Դ���������ʣ��ݷ������֣����������ʽ��������������ʽ�ʼ������ij�ֺ�����ϵ�������±���ʾ��
���������ʽ������������ʽ���ձ�������λ����Ԫ��
��2007���������ʵ�Ͷ���ߴ�2008����ÿ�깲�ɻ��0.67��Ԫ�Ļر�������2007�������������ʽ�����10�귽���ջأ�
��1����������2006��Խ�����Ͷ��Ϊ������Ԫ��
��2�������������ʽ�y����λ����Ԫ���������������x����λ����Ԫ��֮��ĺ�����ϵʽ��
��3����2007������������������в����������ʽ�ķ�Χ��
����Ŀ��Ϊ��Ӧ���ҽ��ܼ��ŵĺ��٣����������Լ�õ磬��ʡ���Ⱥ��̨�������ݼ۸����ƶȣ��������ij�еĵ�۱���ÿ�£�
���� | ����x����λ���ȣ� | ��Ѽ۸�λ��Ԫ/�ȣ� |
һ�� | 0��x��180 | a |
���� | 180��x��400 | b |
���� | x��400 | 0.95 |
��1����֪��Ůʿ�����·��õ�256�ȣ����ɵ��154.56Ԫ�����·��õ�318�ȣ����ɵ��195.48Ԫ��������������ݣ���������е�a��b��ֵ��
��2��5�·ݿ�ʼ�õ����࣬��Ůʿ���ɵ��280Ԫ�����Ůʿ��5�·ݵ��õ�����