题目内容
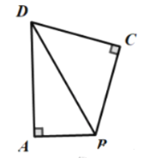
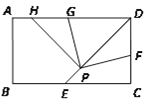
【题目】如图,已知在矩形ABCD中,∠ADC的平分线DE与BC边交于点E,点P是线段DE上一定点(其中EP<PD). 若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交线段DA于点H、G.
(1) 求证:PG=PF;
(2) 探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.

【答案】(1)证明见解析;(2)结论: ![]() ,证明见解析.
,证明见解析.
【解析】(1)∵四边形ABCD是矩形,∴∠ADC=90°,
∵DE平分∠ADC,∴∠PDF=∠ADP=45°,
由旋转可知∠GPF=∠HPD=90°,
∴∠GPH=∠FPD ,
∵∠HPD=90°,∠ADP=45°,
∴△HPD为等腰直角三角形 ,
∴∠DHP=∠PDF=45°且PH=PD ,
∴△HPG≌△DPF ,
∴PG=PF ;
(2)结论: ![]() ,
,
∵△HPD为等腰直角三角形,
∴ HD2=2![]() ,
,
∴![]() ,
,
∵△HPG≌△DPF,
∴DF=HG,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】平价大药房准备购进![]() 、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用
、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用![]() 元购进一次性医用口罩的数量是用
元购进一次性医用口罩的数量是用![]() 元购进
元购进![]() 口罩的数量的
口罩的数量的![]() 倍.
倍.
| 一次性医用口罩 | |
进价(元 |
|
|
售价(元 |
|
|
(1)求![]() 的值;
的值;
(2)要使购进的![]() 、一次性医用两种口罩共
、一次性医用两种口罩共![]() 个的总利润不少于
个的总利润不少于![]() 元,且不超过
元,且不超过![]() 元,问该药店共有多少种进货方案?
元,问该药店共有多少种进货方案?