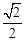题目内容
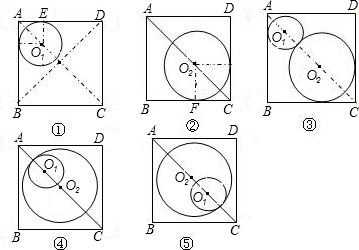
如图:已知正方形ABCD的对角线AC长为20cm,半径为1的⊙O1的圆心O1从A点出发以1cm/s的速度向C运动,半径为1的⊙O2的圆心O2从C点出发以2cm/s的速度向A运动且半径同时也以1cm/s的速度不断增大,两圆同时运动,当其中一个圆的圆心运动到AC的端点时,另一个圆也停止运动.
(1)当O1运动了几秒时,⊙O1与AD相切?
(2)当O2运动了几秒时,⊙O2与CB相切?
(3)当O2运动了几秒时,⊙O1与⊙O2相切?

(1)当O1运动了几秒时,⊙O1与AD相切?
(2)当O2运动了几秒时,⊙O2与CB相切?
(3)当O2运动了几秒时,⊙O1与⊙O2相切?
(1)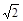 (2)
(2)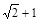 (3)4.5秒、5秒、10秒
(3)4.5秒、5秒、10秒
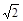 (2)
(2)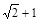 (3)4.5秒、5秒、10秒
(3)4.5秒、5秒、10秒试题分析:
解:(1)设⊙O1运动了t秒时⊙O1与AD相切于E连接OE,∴OE⊥AD,∵AC为正方形的对角线,∴△A O1E为等腰直角三角形,∴AE=O1E=1,∵A O1=t∴t2=12+12,解得t1=
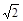 ,t2=-
,t2=-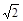 (舍去),当O1运动了
(舍去),当O1运动了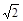 秒时⊙O1与AD相切;
秒时⊙O1与AD相切;(2)设O2运动了t秒时,⊙O2与BC相切于F,则△C O2F为等腰直角三角形,
∴CF=O2F=t+1,∵C O2=2t,∴(2t)2=(t+1)2+(t+1)2
解得t1=
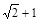 ,t2=
,t2=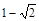 (舍去),∴当O2运动了(
(舍去),∴当O2运动了(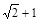 )秒时,⊙O2与BC相切;
)秒时,⊙O2与BC相切;(3)设运动了t秒时⊙O1,⊙O2相切,则O1A=t,O2C=2t,①如图③⊙O1与⊙O2第一次相切时,则O1 O2=1+t+1,∵O1 O2=AC-O1A-O2C,∴1+t+1=20-t-2t,解得t=
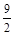 ,
,②如图④⊙O1与⊙O2第二次相切时则O1 O2=t+1-1,∵O1 O2=20-t-2t,∴t+1-1=20-t-2t 解得t=5,(2分)
③如图⑤⊙O1与⊙O2第三次相切时则O1 O2=t+1-1=t,∵O1 O2=O1A-O2C-AC=t+2t-20,∴t=t+2t-20, 解得t=10,∵t=10时,O2C=2×10=20∴此时O2落在AC的端点A上,(2分)∴当运动了4.5秒、5秒、10秒时⊙O1与⊙O2相切.
点评:该题运用的知识点较为简单,两圆相切,半径的关系要清楚,相切有内切和外切,学生要分情况分析。

练习册系列答案
相关题目
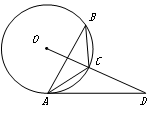
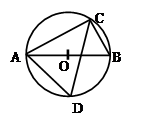
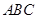 为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.
为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.