题目内容
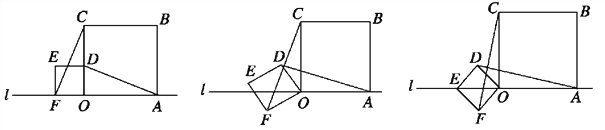
【题目】数轴上有两点A，B， 点C，D分别从原点O与点B出发，沿BA方向同时向左运动.
（1）如图，若点N为线段OB上一点，AB=16，ON=2，当点C，D分别运动到AO，BN的中点时，求CD的长；
（2）若点C在线段OA上运动，点D在线段OB上运动，速度分别为每秒1cm, 4cm，在点C，D运动的过程中，满足OD=4AC，若点M为直线AB上一点，且AM-BM=OM，求
的值.
【答案】（1）9；（2）
或1.
【解析】
（1）根据C，D分别为AO，BN的中点，可得ND=
BN，CO=AO，再根据CD=CO+ON+DN，将ND，CO代入可得出结果；
（2）根据OD=4AC，BD=4CO,可得出OA:OB=1：4. 由点M为直线AB上一点，且AM-BM=OM，分两种情况求解：①当点M在线段AB上，先由已知等量关系得出AO=BM，设AO=x，再用x表示出AB，OM即可得出结果；②当点M在B点右侧时，由. AM-BM=AB=OM可得出结果.
解：（1）当点C，D分别运动到AO，BN的中点时，得
ND=BN，CO=AO，
∴CD=CO+ON+DN=AO+ON+BN=(AO+BN)+ON=(AB-ON)+ON，
又AB=16，ON=2，
∴CD=×（16-2）+2=9.
（2）∵C,D两点运动的速度比为1:4，∴BD=4CO.
又OD=4AC，∴BD+OD=4（CO+AC）,
∴OB=4OA，即OA:OB=1：4.
若点M为直线AB上一点，且AM-BM=OM，
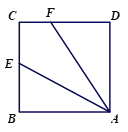
①点M在线段AB上时，如图，
∵AM-BM=OM，∴AO+OM-BM=OM，
∴AO=BM，
设AO=x，则BM=x，
由OA:OB=1：4，得BO=4x，AB=5x
∴OM=BO-BM=3x，
∴
.
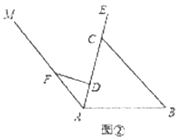
②当点M在B点右侧时，如图，
∵AM-BM=OM，
∴AB=OM，
∴
综上所述：
的值为或1.
