题目内容
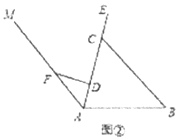
【题目】“4000辆自行车、187个服务网点”,某市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便。图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=30 cm,DF=20 cm,AF=25 cm,FD⊥AE于点D,座杆CE=15 cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

【答案】(1)15cm;(2)点E到AB的距离为58.2cm
【解析】分析:(1)根据勾股定理求出AD的长;
(2)作EH⊥AB于H,求出AE的长,根据正弦的概念求出点E到车架AB的距离.
详解:(1)在Rt△ADF中,由勾股定理得,
AD=![]() (cm).
(cm).
(2)AE=AD+CD+EC=15+30+15=60(cm).
过点E作EH⊥AB于H,

在Rt△AEH中,sin∠EAH=![]() ,
,
∴EH=AEsin∠EAH=ABsin75°≈60×0.97=58.2(cm).
答:点E到AB的距离为58.2cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目