题目内容
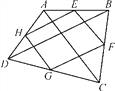
【题目】已知：如图，在ABCD中，点E在AD上，连接BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N，AF，BE分别平分∠BAD，∠ABC；CE，DF分别平分∠BCD，∠ADC，则四边形MFNE是（ ）
A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
【答案】B
【解析】分析：首先根据平行四边形的判定得出四边形BEDF和四边形AFCE是平行四边形，然后得出四边形MFNE是平行四边形，根据角平分线的性质得出∠BEC=90°，从而说明四边形MFNE是矩形．
详解：∵四边形ABCD是平行四边形， ∴AD=BC，AD∥BC， 又∵DF∥BE，
∴四边形BEDF是平行四边形， ∴DE=BF，ME∥NF，∴AD-DE=BC-BF，即AE=CF，
又∵AE∥CF， ∴四边形AFCE是平行四边形， ∴MF∥NE，
∴四边形MFNE是平行四边形， ∵BE、CE是角平分线，
∴∠EBC+∠ECB=180°×
=90°，∴∠BEC=90°，∴四边形MFNE是矩形，故选B．
练习册系列答案
相关题目
