题目内容
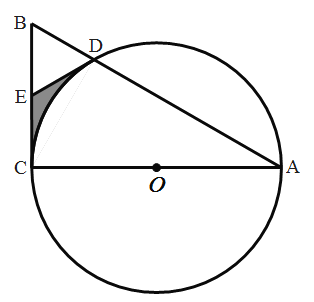
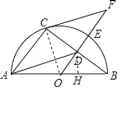
【题目】如图,AB是半圆O的直径,D为弦BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC,
(1)求证:CF为⊙O的切线;
(2)若四边形ACFD是平行四边形,求sin∠BAD的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OC,根据等腰三角形的性质得到∠OCB=∠B,∠OCB=∠F,根据垂径定理得到OF⊥BC,根据余角的性质得到∠OCF=90°,于是得到结论;
(2)过D作DH⊥AB于H,根据三角形的中位线的想知道的OD=![]() AC,根据平行四边形的性质得到DF=AC,设OD=x,得到AC=DF=2x,根据射影定理得到CD=
AC,根据平行四边形的性质得到DF=AC,设OD=x,得到AC=DF=2x,根据射影定理得到CD=![]() x,求得BD=
x,求得BD=![]() x,根据勾股定理得到AD=
x,根据勾股定理得到AD=![]() x,于是得到结论.
x,于是得到结论.
解:(1)连接OC,
∵OC=OB,
∴∠OCB=∠B,
∵∠B=∠F,
∴∠OCB=∠F,
∵D为BC的中点,
∴OF⊥BC,
∴∠F+∠FCD=90°,
∴∠OCB+∠FCD=90°,
∴∠OCF=90°,
∴CF为⊙O的切线;
(2)过D作DH⊥AB于H,
∵AO=OB,CD=DB,
∴OD=![]() AC,
AC,
∵四边形ACFD是平行四边形,
∴DF=AC,
设OD=x,
∴AC=DF=2x,
∵∠OCF=90°,CD⊥OF,
∴CD2=ODDF=2x2,
∴CD=![]() x,
x,
∴BD=![]() x,
x,
∴AD=![]() x,
x,
∵OD=x,BD=![]() x,
x,
∴OB=![]() x,
x,
∴DH=![]() x,
x,
∴sin∠BAD=![]() =
=![]() .
.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目