题目内容
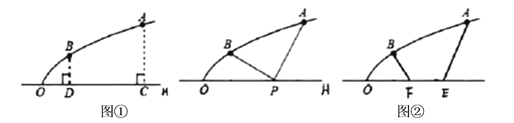
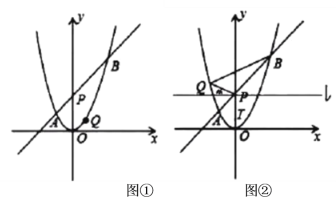
【题目】如图①,在平面直角坐标系中,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,将直线
,将直线![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 的度数后与该抛物线交于
的度数后与该抛物线交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 是该抛物线上一点
是该抛物线上一点
(1)若![]() ,求直线
,求直线![]() 的函数表达式
的函数表达式
(2)若点![]() 将线段分成
将线段分成![]() 的两部分,求点
的两部分,求点![]() 的坐标
的坐标
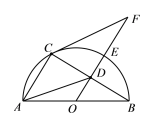
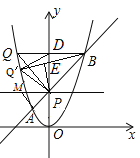
(3)如图②,在(1)的条件下,若点![]() 在
在![]() 轴左侧,过点
轴左侧,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是直线
是直线![]() 上一点,且位于
上一点,且位于![]() 轴左侧,当以
轴左侧,当以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,求
相似时,求![]() 的坐标
的坐标
【答案】(1)![]() ;(2)
;(2)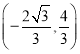 或
或![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;
(2)分![]() 和
和![]() 两种情况根据点A、点B在直线y=x+2上列式求解即可;
两种情况根据点A、点B在直线y=x+2上列式求解即可;
(3)分![]() 和
和![]() 两种情况,利用相似三角形的性质列式求解即可.
两种情况,利用相似三角形的性质列式求解即可.
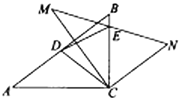
(1)如图①,设直线AB与x轴的交点为M.
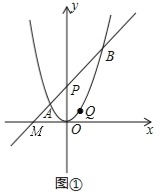
∵∠OPA=45°,
∴OM=OP=2,即M(-2,0).
设直线AB的解析式为y=kx+b(k≠0),将M(-2,0),P(0,2)两点坐标代入,得
![]() ,
,
解得,![]() .
.
故直线AB的解析式为y=x+2;
(2)①![]()
设![]()
![]() (a>0)
(a>0)
∵点A、点B在直线y=x+2上和抛物线y=x2的图象上,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
解得,![]() ,
,![]() (舍去)
(舍去)
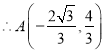
②![]()
设![]()
![]() (a>0)
(a>0)
∵点A、点B在直线y=x+2上和抛物线y=x2的图象上,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
解得:![]() ,
,![]() (舍去)
(舍去)
![]()
综上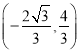 或
或![]()
(3)![]() ,
,![]()
![]() ,
,![]()
①![]()
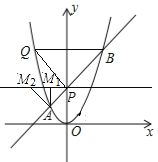
此时![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,![]() 为等腰直角三角形
为等腰直角三角形
![]()
![]()
②![]()
此时![]() 满足,左侧还有
满足,左侧还有![]() 也满足
也满足
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,易得圆心为
四点共圆,易得圆心为![]() 中点
中点![]()
设![]() ,
,![]()
∵![]()
![]()
![]()
![]() 且不与
且不与![]() 重合
重合
![]()
![]() ,
,![]()
![]()
![]() 为正三角形,
为正三角形,
![]()
过![]() 作
作![]() ,则
,则![]() ,
,![]()
![]()
∵![]()
∴![]()
∴![]()
解得,![]()
∴![]()
∵![]()
∴![]()
∴![]()
解得,![]()
∴![]()
综上所述,满足条件的点M的坐标为:![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目