题目内容
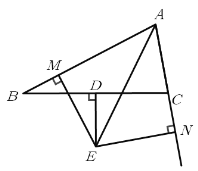
【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为_________.
【答案】3或6.
【解析】
如图1,所示,由∠CFE+∠AFE=180°,可知点A、F、C在一条直线上,先求得AC的长,然后由△AEF∽△ACD可求得ED的长;如图2所示,可证明四边形CDEF为正方形从而可求得ED的长.
如图1所示:
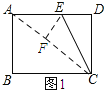
由翻折的性质可知:EF=ED,∠EFC=∠EDC=90°,
∵△AEF为直角△,
∴∠AFE=90°.
∴∠CFE+∠AFE=180°.
∴点A、F、C在一条直线上.
在Rt△ABC中,AC=![]() =10.
=10.
设DE=x,则EF=x.
∵∠EAF=∠DAC,∠EFA=∠CDA,
∴△AEF∽△ACD.
∴![]() ,即
,即![]() .
.
解得:x=3.
∴ED=3.
如图2所示:
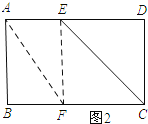
∵∠AEF=90°,
∴∠FED=90°.
∴∠FED=∠D=∠DCF=90°.
∴四边形CDEF为矩形.
由翻折的性质可知:DE=EF.
∴四边形CDEF为正方形.
∴DE=DC=6.
综上所述,ED的长为3或6.
故答案为:3或6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目