题目内容
【题目】已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC﹣∠CEF=90°,连接AF,M是AF的中点
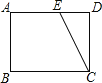
(1)如图1,当CB与CE在同一直线上时,连接CM,若CB=1,CE=2,求CM的长.
(2)如图2,连接MB,ME,当∠BCE=45°时,求证:BM=ME.

【答案】(1)![]() .(2)证明见解析.
.(2)证明见解析.
【解析】
(1)首先利用勾股定理得出AF的长,再利用直角三角形斜边的中线等于斜边的一半来解答即可;(2) 连接BE、DE,先由△ABM≌△FDM,得出AB=DF,BM=DM,进而得出AB=BC=DF,再经过证明△BCE≌△DFE,得出△BDE是等腰直角三角形即可求解.
(1)解:∵△ABC是等腰三角形,CB=1,
∴∠ACB=45°,AC=![]() ,
,

∵△CEF是等腰直角三角形,CE=2
∴∠ECF=45°,CF=2![]() ,
,
∴∠ACF=∠ACB+∠ECF=45°+45°=90°,
∴AF2=AC2+CF2=10,
∵M是AF的中点,
∴CM=![]() AF=
AF=![]() .
.
(2)证明:由此BM交CF于D,连接BE、DE.
∵∠BCE=45°,
∴∠ACD=45°×2+45°=135°,
∴∠BAC+∠ACF=45°+135°=180°,
∴AB∥CF,
∴∠BAM=∠DFM,
∵M是AF的中点,
∴AM=FM,
在△ABM和△FDM中, ,
,
∴△ABM≌△FDM(ASA),
∴AB=DF,BM=DM,
∴AB=BC=DF,
在△BCE和△DFE中, ,
,
∴△BCE≌△DFE(SAS),
∴BE=DE,∠BEC=∠DEF,
∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°,
∴△BDE是等腰直角三角形,
∵BM=MD,
∴BM=ME=![]() BD,
BD,
∴BM=ME.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目