题目内容
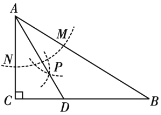
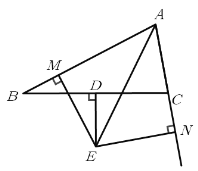
【题目】如图所示,BD=DC,DE⊥BC,交∠BAC的平分线于E,EM⊥AB,EN⊥AC,
(1)求证:BM=CN
(2)若AB=9,AC=5.求AM长.
【答案】(1)见解析;(2)7;
【解析】
(1)连接BE、EC,由中垂线的性质就可以得出BE=CE,由EM⊥AB,EN⊥AC,AE平分∠BAC由角平分线的性质就可以得出EM=EN,在证明Rt△BME和Rt△CNE全等及可以得出结论.
(2)过点E作EM⊥AC的延长线于点M,连接BE、EC,利用角平分线的性质、垂直平分线的性质得到EM=EN,EB=EC,证明Rt△BME≌Rt△CNE(HL),得到BM=CN,证明Rt△AME≌Rt△ANE(HL),得到AM=AN,由AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,即AM=9-AM+5,即可解答.
(1)证明:连接BE、EC,
∵BD=DC,DE⊥BC
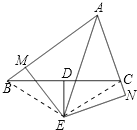
∵BE=EC.
∵AE平分∠BAC,EM⊥AB,EN⊥AC,
EM=EN,∠EMB=∠ENC=90°.
在Rt△BME和Rt△CNE中,
∵BE=EC,EM=EN
![]() ,
,
∴Rt△BME≌Rt△CNE(HL)
∴BM=CN.
(2)如图,过点E作EM⊥AC的延长线于点M,连接BE、EC,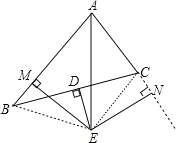
由(1)可知Rt△BME≌Rt△CNE(HL)
∴BM=CN,
在RtAME和Rt△ANE中,![]() ,
,
∴Rt△AME≌Rt△ANE(HL)
∴AM=AN,
∴AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,
即AM=9-AM+5
2AM=9+5
2AM=14
AM=7.

【题目】有20筐白菜,以每筐25千克为标准,超过或不足千克数分别用正,负数表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?