题目内容
【题目】如图，已知数轴上依次有三点 A、B、C，点 B 对应的数是
，且点 B 到点A、C的距离均为600.
(1)写出点A所对应的数；
(2)若动点P、Q分别从B、C两点同时向右运动，点 P、Q 的速度分别为 10 单位长度每秒、5单位长度每秒，问多少秒时点P与点Q重合；
(3)若动点P、Q分别从A、C两点相向而行，点P运动20秒后，点Q开始运动，点P、Q的速度分别为10单位长度每秒、5单位长度每秒，问点 P 运动多少秒时P，Q两点的距离为200.
【答案】（1）
；（2）120秒；（3）运动73.3或100秒时PQ距离为200.
【解析】
(1)根据求数轴上两点之间的距离的方法计算.
(2)根据追及问题的计算公式，路程差=速度差
时间，直接计算或者列方程解答即可.
(3)首先要想到问题P，Q两点的距离为200有两种情况，即P，Q相遇之前和相遇之后，再根据相遇问题的计算公式，路程和=甲运动路程+乙运动路程，路程=速度时间，直接计算或者列方程解答.
（1）由题意得，
，所以点A所对应的数.
（2）点 P 与点 Q 运动的路程差为 600，速度差为 5，故
，
则120秒后P、Q两点重合.
另解：假设运动 x 秒时 P、Q 重合，
则有
.解得
(3)PQ 距离为 200 时有两种情况：
相遇前（Q 在 P 的右边）：
相遇后（P 在Q的右边）：
故运动73.3或100秒时PQ距离为 200.
智趣寒假作业云南科技出版社系列答案【题目】为选派一名学生参加全市实践活动技能竞赛，A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm）
平均数 | 方差 | 完全符合要求个数 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
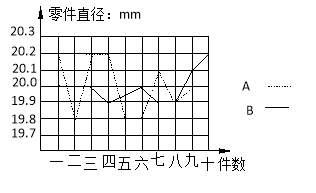
根据测试得到的有关数据，试解答下列问题：
⑴ 考虑平均数与完全符合要求的个数，你认为 的成绩好些；
⑵ 计算出SB2的大小，考虑平均数与方差，说明谁的成绩好些；
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由。
【题目】有20筐白菜，以每筐25千克为标准，超过或不足千克数分别用正，负数表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐多重多少千克？
（2）与标准质量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.8元，则出售这20筐白菜可卖多少元？
