题目内容
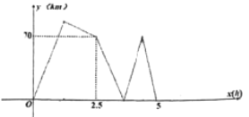
【题目】甲乙两地相距300
，一辆货车和一辆轿车先后从甲地出发到乙地停止，货车先出发从甲地匀速开往乙地，货车开出一段时间后，轿车出发，匀速行驶一段时间后接到通知提速后匀速赶往乙地（提速时间不计），最后发现轿车比货车提前0.5小时到达，下图表示两车之间的距离
与货车行驶的时间
之间的关系，则货车行驶__________小时．两车在途中相遇．
【答案】3.9
【解析】
根据题意和函数图象中的数据可以求得货车的速度和轿车提速后的速度，从而可以求得货车行驶多长时间，两车在途中相遇.
由题意，得
货车的速度为：300÷5=60km/h
货车2.5小时行驶的路程是：60×2.5=150km
则小轿车提速后的速度为：
km/h
设货车行驶
小时，两车在途中相遇，
解得
故答案为：3.9.
练习册系列答案
名校课堂系列答案
相关题目
【题目】参照学习函数的过程与方法，探究函数
的图象与性质．因为
，即
，所以我们对比函数
来探究．
列表：
| … | -4 | -3 | -2 | -1 |
|
|
| 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 | -4 | -1 |
| … | ||
| … |
|
| 2 | 3 | 5 | -3 | -1 | 0 |
|
| … |
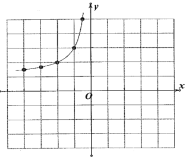
描点：在平面直角坐标系中，以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点，如图所示：
（1）①请补全表格，计算
__________．
②请补全图形，用一条光滑曲线顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，
随的增大而__________；（填“增大”或“减小”）
②的图象是由的图象向__________平移__________
③图象关于点__________中心对称．（填点的坐标）
（3）结合函数图象，当
时，求的取值范围．
