Question

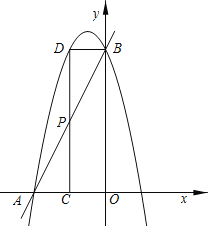
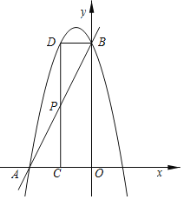
【题目】如图，已知直线y＝2x+4分别交x轴，y轴于点A，B，抛物线过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．

（1）若抛物线的解析式为y＝﹣2x2﹣2x+4，设其顶点为M，其对称轴交AB于点N．

①直接写出点M，N的坐标．

②若四边形MNPD为平行四边形，请求出点P的坐标．

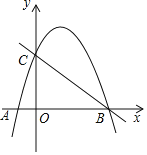
（2）当点P的横坐标为﹣1时，是否存在这样的抛物线，使得以B，P，D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．

Answer 1

【答案】（1）①M， N；②P；（2）存在，y＝﹣2x2﹣2x+4或y＝﹣x2﹣3x+4．

【解析】

（1）①抛物线的对称轴为：直线x＝﹣，进而，即可求解；②PD＝﹣2m2﹣2m+4﹣（2m+4）＝﹣2m2﹣4m，当PD＝MN时，四边形MNPD为平行四边形，即可求解；

（2）分 、两种情况，分别求解即可．

（1）①抛物线的对称轴为：直线x＝﹣，则点M的坐标为（﹣，），

当x＝﹣时，y＝2x+4＝3，

∴点N（﹣，3）；

②∵M（﹣，），N（﹣，3），

∴MN＝﹣3＝．

设P点坐标为（m，2m+4），则D（m，﹣2m2﹣2m+4），

∴PD＝﹣2m2﹣2m+4﹣（2m+4）＝﹣2m2﹣4m，

∵PD∥MN，

∴当PD＝MN时，四边形MNPD为平行四边形，即﹣2m2﹣4m＝，

解得：m1＝﹣（舍去），m2＝﹣．

∴P点坐标为（﹣，1）；

（2）存在．如图，OB＝4，OA＝2，则AB＝．

∵当x＝﹣1时，y＝2x+4＝2，

∴P（﹣1，2），

∴PB＝．

设抛物线的解析式为y＝ax2+bx+4，

把A（﹣2，0）代入得：4a﹣2b+4＝0，解得：b＝2a+2．

∴抛物线的解析式为：y＝ax2+2（a+1）x+4，

∴当x＝﹣1时，y＝ax2+2（a+1）x+4＝a﹣2a﹣2+4＝2﹣a，

即：D（-1，2﹣a）．

∴PD＝2﹣a﹣2＝﹣a，

∵DC∥OB，

∴∠DPB＝∠OBA．

①当时，△PDB∽△BOA，即 ，解得a＝﹣2．

此时抛物线解析式为：y＝﹣2x2﹣2x+4；

②当时，△PDB∽△BAO，即，解得a＝﹣．

此时抛物线解析式为：y＝﹣x2﹣3x+4；

综上所述，所求抛物线的解析式为：y＝﹣2x2﹣2x+4或y＝﹣x2﹣3x+4．