题目内容
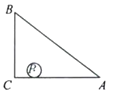
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,圆
,圆![]() 在
在![]() 内自由移动.若
内自由移动.若![]() 的半径为1,则圆心
的半径为1,则圆心![]() 在
在![]() 内所能到达的区域的面积为______.
内所能到达的区域的面积为______.
【答案】24
【解析】
根据题意做图,圆心![]() 在
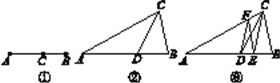
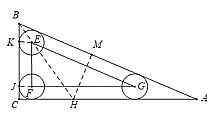
在![]() 内所能到达的区域为△EFG,先求出AB的长,延长BE交AC于H点,作HM⊥AB于M,根据圆的性质可知BH平分∠ABC,故CH=HM,设CH=x=HM,根据Rt△AMH中利用勾股定理求出x的值,作EK⊥BC于K点,利用△BEK∽△BHC,求出BK的长,即可求出EF的长,再根据△EFG∽△BCA求出FG,即可求出△EFG的面积.
内所能到达的区域为△EFG,先求出AB的长,延长BE交AC于H点,作HM⊥AB于M,根据圆的性质可知BH平分∠ABC,故CH=HM,设CH=x=HM,根据Rt△AMH中利用勾股定理求出x的值,作EK⊥BC于K点,利用△BEK∽△BHC,求出BK的长,即可求出EF的长,再根据△EFG∽△BCA求出FG,即可求出△EFG的面积.
如图,由题意点O所能到达的区域是△EFG,连接BE,延长BE交AC于H点,作HM⊥AB于M,EK⊥BC于K,作FJ⊥BC于J.
∵![]() ,
,![]() ,
,![]() ,
,
∴AB=![]()
根据圆的性质可知BH平分∠ABC
∴故CH=HM,设CH=x=HM,则AH=12-x,BM=BC=9,
∴AM=15-9=6
在Rt△AMH中,AH2=HM2+AM2
即AH2=HM2+AM2
(12-x)2=x2+62
解得x=4.5
∵EK∥AC,
∴△BEK∽△BHC,
∴![]() ,即
,即![]()
∴BK=2,
∴EF=KJ=BC-BK-JC=9-2-1=6,
∵EG∥AB,EF∥AC,FG∥BC,
∴∠EGF=∠ABC,∠FEG=∠CAB,
∴△EFG∽△ACB,
故![]() ,即
,即![]()
解得FG=8
∴圆心![]() 在
在![]() 内所能到达的区域的面积为
内所能到达的区域的面积为![]() FG×EF=
FG×EF=![]() ×8×6=24,
×8×6=24,
故答案为24.

练习册系列答案
相关题目