Question

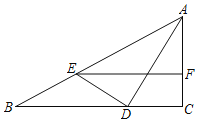
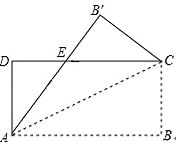
【题目】如图，将矩形沿对角线折叠，点的对应点为点，与相交于点，若，，则的长度是( ）

A.1B.2C.D.3

Answer 1

【答案】A

【解析】

在矩形ABCD中，在矩形ABCD中，∠B=90°，，得到=30°，求得BC=，根据折叠的性质得到A=AB=3，∠AC=∠BAC，推出AF=CF，设DF=m，则AF=CF=3m，，根据勾股定理结论得到结论．

解：在矩形ABCD中，∠B=90°，
∵AB=3，，

∴=30°，
∴BC=AB=，

∵△ABC沿对角线对折，得到△AC，
∴A=AB=3，∠AC=∠BAC，
∵AB//DC，
∴∠BAC=∠DCA，
∴∠AC=∠DCA，
∴AF=CF，
设DF=m，则AF=CF=3m，
∵AD2+DF2=AF2，
∴()2+m2=(3m)2，
∴m=1，
故选A．