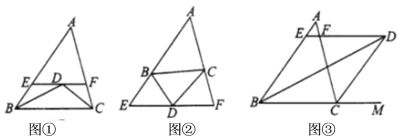Question

【题目】在四边形ABCD中，AD=6,BC=4,E、F分别是AB、CD的中点，则线段EF的取值范围是_____．

Answer 1

【答案】1<EF<5

【解析】

设G是BD的中点，连接EG、FG，根据三角形的中位线定理，求出EG、FG的长度各是多少；然后在△EFG中，根据任意两边之和大于第三边三边，任意两边之差小于第三边，求出线段EF长的取值范围即可．

如图所示：G是BD的中点，连接EG、FG

∵E是AB的中点，G是BD的中点，
∴EG∥AB，且EG=AD=×6＝3；
∵F是BC的中点，G是BD的中点，
∴FG∥CD，且FG=BC=×4＝2；
∵FG-EG=3-2=1，FG+EG=3+2=5，
所以EF的取值范围为1<EF<5.

故答案是：1<EF<5.