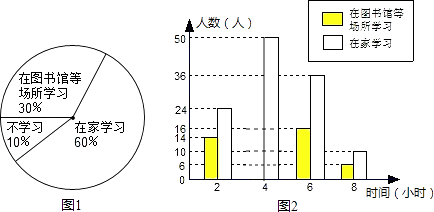
��Ŀ����
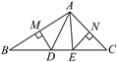
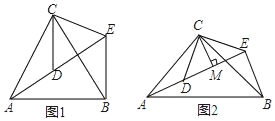
����Ŀ����1������̽������ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
����֤����CDA�ա�CEB��
�����AEB�Ķ�����
��2�������ʽ����ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE��
���������AEB�Ķ���
��ֱ��д���߶�AE��CM��BE֮���������ϵ������˵�����ɣ�
���𰸡���1����֤������������60�㣻��2����90�㣻��AE= BE+2CM
��������
��1���ٸ��ݵȱ������ε����ʵõ�CA=CB=AB��CD=CE=DE����ACB=��DCE=60��������SAS����֤����CDA�ա�CEB��
�ڸ���ȫ�������ε����ʵõ���CEB=��ADC=120�������ͼ�μ��㼴�ɣ�
��2���ٸ��ݵ���ֱ�������ε����ʵõ�CA=CB��CD=CE����ACD=��BCE������SAS����֤����CDA�ա�CEB������ȫ�������ε����ʼ��㼴�ɣ�
�ڸ���ȫ�������ε����ʵõ�BE=AD������ֱ�������ε����ʵõ�DE=2CM�����ͼ�ν��
��1����֤�����ߡ�ACB����DCE��Ϊ�ȱ������Σ�
��CA=CB=AB��CD=CE=DE����ACB=��DCE=60�㣬
���ACB����DCB=��DCE����DCB������ACD=��BCE��
����CDA����CEB��
 ��
��
���CDA�ա�CEB��
�ڽ⣺�ߡ�CDE=60�㣬
���ADC=120�㣬
�ߡ�CDA�ա�CEB��
���CEB=��ADC=120�㣬
���AEB=120�㩁60��=60�㣻
��2���١ߡ�ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬
��CA=CB��CD=CE����ACB����DCB=��DCE��DCB������ACD=��BCE��
����CDA����CEB��
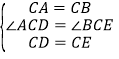 ��
��
���CDA�ա�CEB��
���CEB=��ADC=135�㣬
���AEB=135�㩁45��=90�㣻
�ڽ⣺�ߡ�CDA�ա�CEB��
��BE=AD��
��CD=CE��CM��DE��
��DM=ME���֡�DCE=90�㣬
��DE=2CM��
��AE=AD+DE=BE+2CM��