题目内容
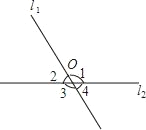
【题目】如图所示,直线l1与l2相交于点O,且∠1+∠3=2(∠2+∠4),求下列角的度数.(1)∠2+∠4;(2)∠1,∠2.
【答案】(1)∠2+∠4=120°;(2)∠1=120°,∠2=60°.
【解析】
(1)根据∠1与∠2、∠3与∠4互为邻补角得∠1=180°-∠2,∠3=180°-∠4,将∠1、∠3代入∠1+∠3=2(∠2+∠4),可得∠2+∠4度数;
(2)根据对顶角相等有∠2=∠4,又由(1)知∠2+∠4=120°,故∠2=∠4=60°,进而得到∠2的邻补角∠1=120°.
(1)∵∠1与∠2、∠3与∠4互为邻补角,
∴∠1=180°﹣∠2,∠3=180°﹣∠4,
∵∠1+∠3=2(∠2+∠4),
∴180°﹣∠2+180°﹣∠4=2(∠2+∠4),即360°﹣(∠2+∠4)=2(∠2+∠4),
∴3(∠2+∠4)=360°,
故∠2+∠4=120°;
(2)∵∠2与∠4是对顶角,
∴∠2=∠4,
由(1)知,∠2+∠4=120°,
∴2∠2=120°,故∠2=60°,
∵∠1=180°﹣∠2,
∴∠1=120°,
故∠1=120°,∠2=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目