题目内容
【题目】请在横线上填写合适的内容,完成下面的证明:
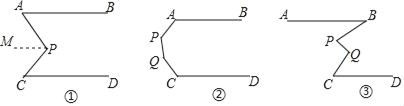
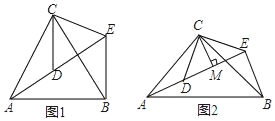
(1)如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB,
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以PM∥CD( )
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C( )
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)
【答案】(1)两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠CPM;两直线平行,内错角相等;等量代换;(2)540°;(3)x﹣y+z.
【解析】
(1)根据平行线的性质和判定填
(2)过点P作PE∥AB,过点Q作QF∥AB,根据平行线的性质可求.
(3)过点P作PE∥AB,过点Q作QF∥AB,根据平行线的性质可求.
(1)过P作PM∥AB,
所以∠A=∠APM,(两直线平行,内错角相等),
因为PM∥AB,AB∥CD(已知),
所以PM∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠C=∠CPM(两直线平行,内错角相等),
因为∠APC=∠APM+∠CPM,
所以∠APC=∠A+∠C(等量代换),
故答案为:两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠CPM;两直线平行,内错角相等;等量代换.
(2)如图过点P作PE∥AB,过点Q作QF∥AB
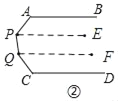
∵AB∥DC,PE∥AB,QF∥AB,
∴AB∥PE∥QF∥CD,
∴∠A+∠APE=180°,
∠EPQ+∠PQF=180°,
∠FQC+∠QCD=180°,
∴∠A+∠APQ+∠PQC+∠C=540°,
故答案为:540°;
(3)如图:过点P作PE∥AB,过点Q作QF∥AB,
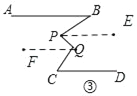
∵AB∥DC,PE∥AB,QF∥AB,
∴AB∥PE∥QF∥CD,
∴∠B=∠BPE,∠BPE=∠PQF,∠FQC=∠C,
∴∠B+∠PQC=∠C+∠BPQ,
即x+z=m+y,
m=x﹣y+z,
故答案为x﹣y+z.