题目内容
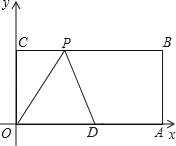
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在边BC上运动,当△ODP是腰长为10的等腰三角形时,则P点的坐标为_____.
【答案】(6,8)或(8,8)或(16,8).
【解析】
此题分二种情况(1)OD是等腰三角形的底边时,(2)OD是等腰三角形的一条腰时,①若点O是顶角顶点时,②若D是顶角顶点时,分别进行讨论得出P点的坐标,再选择即可.
(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠10;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以10为半径的弧与CB的交点,在直角△OPC中,CP=![]() =6,
=6,
则P的坐标是(6,8);
②若D是顶角顶点时,P点就是以点D为圆心,以10为半径的弧与CB的交点,
过D作DM⊥BC于点M,
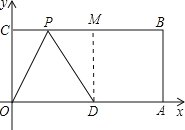
在直角△PDM中,PM=![]() =6,
=6,
当P在M的左边时,CP=10-6=4,则P的坐标是(4,8);
当P在M的右侧时,CP=5+3=8,则P的坐标是(16,8);
故P的坐标为:(6,8)或(8,8)或(16,8);
故答案为:(6,8)或(8,8)或(16,8).

练习册系列答案
相关题目