题目内容
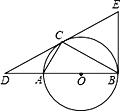
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
【答案】(1)![]() ;(2)直线EB与
;(2)直线EB与![]() 相切,证明见解析.
相切,证明见解析.
【解析】试题分析:(1)根据DA:AB=1:2,得到DA等于圆的半径.连接过切点的半径,构造直角三角形,利用解直角三角形的知识求解;
(2)连接OC.根据(1)中的结论,可以知道直角![]() 有一个角为30°.根据圆周角定理发现
有一个角为30°.根据圆周角定理发现![]() 得到
得到![]() 进一步得到等边
进一步得到等边![]() .则
.则![]() 根据切线的判定即可证明.
根据切线的判定即可证明.
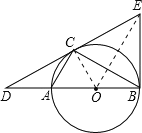
试题解析:(1)如图,连接OC,
∵CD是![]() 的切线,
的切线,
![]()
设![]() 的半径为R,则AB=2R,
的半径为R,则AB=2R,
∵DA:AB=1:2,
∴DA=R,DO=2R.
在Rt△DOC中, ![]()
![]() 即
即![]()
(2)直线EB与![]() 相切,
相切,
证明:连接OC,
由(1)可知![]()
![]()
∵OC=OB,
![]()
∴∠CBD=∠CDB.
∴CD=CB.
∵CD是![]() 的切线,
的切线,
![]()
![]() 又∵CD=CE,
又∵CD=CE,
∴CB=CE.
∴△CBE为等边三角形,
![]()
∴EB是![]() 的切线.
的切线.

练习册系列答案
相关题目