题目内容
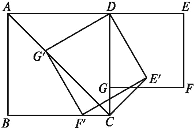
【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
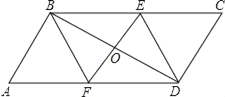
【答案】(1)见解析;(2)EF与BD互相垂直平分;(3)矩形BEDF的面积为8![]() .
.
【解析】
(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;(2)根据根据菱形的性质作出判断:EF与BD互相垂直平分;(3)根据Rt△ABF的边角关系,求得BF和AF,再根据矩形的性质,求得DF的长,最后计算矩形的面积.
(1)∵四边形ABCD是平行四边形,O是BD中点,
∴BC∥AD,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,根据菱形的性质可得:EF与BD互相垂直平分;
(3)∵四边形BEDF是矩形
∴∠AFB=90°
又∵∠A=60°,
∴∠ABF=30°,
∴AF=![]() AB=
AB=![]() ×4=2,
×4=2,
∴Rt△ABF中,BF=2![]() ,
,
又∵AD=BC=6,
∴DF=6﹣2=4,
∴矩形BEDF的面积=BF×DF=2![]() ×4=8
×4=8![]() .
.

练习册系列答案
相关题目
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示:
用电量(千瓦时) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数、平均数分别是( )
A. 180,160,164B. 160,180;164
C. 160,160,164D. 180,180,164