题目内容
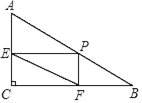
【题目】在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
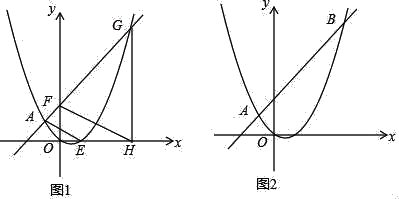
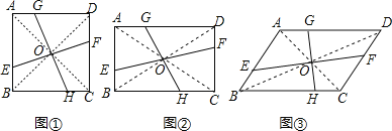
(感知)如图①,若四边形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG,又因为S△AOB=![]() S四边形ABCD,所以S四边形AEOG=
S四边形ABCD,所以S四边形AEOG=![]() S正方形ABCD(不要求证明);
S正方形ABCD(不要求证明);
(拓展)如图②,若四边形ABCD是矩形,且S四边形AEOG=![]() S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
(探究)如图③,若四边形ABCD是平行四边形,且S四边形AEOG=![]() SABCD,若AB=3,AD=5,BE=1,则AG=______.
SABCD,若AB=3,AD=5,BE=1,则AG=______.
【答案】【拓展】AG=![]() ;【探究】
;【探究】![]()
【解析】
拓展:如图②,作高线OM和ON,根据S△AOB=![]() S矩形ABCD,可得S△AOB=S四边形AEOG,所以△BOE和△AOG的面积相等,根据面积公式列式可得AG的长;
S矩形ABCD,可得S△AOB=S四边形AEOG,所以△BOE和△AOG的面积相等,根据面积公式列式可得AG的长;
探究:如图③,同理:过O作QM⊥AB,PN⊥AD,先根据平行四边形面积可得OM和ON的比,同理可得S△BOE=S△AOG,根据面积公式可计算AG的长.
拓展:如图②,过O作OM⊥AB于M,ON⊥AD于N,
∵S△AOB=![]() S矩形ABCD,
S矩形ABCD,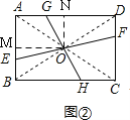
S四边形AEOG=![]() ,
,
∴S△AOB=S四边形AEOG,
∵S△BOE=![]() =
=![]() =
=![]() mb,
mb,
S△AOG=![]() AGON=
AGON=![]() AG
AG![]() =
=![]() AGa,
AGa,
∴![]() mb=
mb=![]() AGa,
AGa,
∴AG=![]() ;
;
探究:
如图③,过O作QM⊥AB,PN⊥AD,
则MQ=2OM,PN=2ON,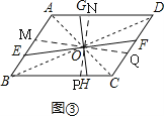
∵SABCD=ABMQ=ADPN,
∴3×2OM=5×2ON,
∴![]() =
=![]() ,
,
∵S△AOB=![]() SABCD,
SABCD,
S四边形AEOG=![]() SABCD,
SABCD,
∴S△AOB=S四边形AEOG,
∵S△BOE=![]() =
=![]() ×1×OM,
×1×OM,
S△AOG=![]() AGON,
AGON,
∴![]() ×1×OM=
×1×OM=![]() AGON,
AGON,
OM=AGON,
![]() =AG=
=AG=![]() ,
,
∴AG=![]() ;
;
故答案为:![]() .
.


 亮点激活精编提优100分大试卷系列答案
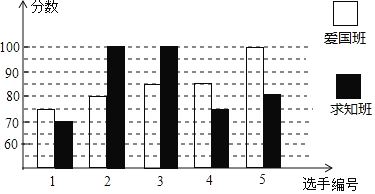
亮点激活精编提优100分大试卷系列答案【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?