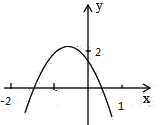��Ŀ����
����Ŀ����֪��A����1��2����B��3��6����������y=ax2+bx��
(1)�������ߵĽ���ʽ��
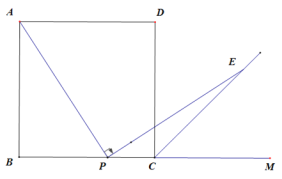
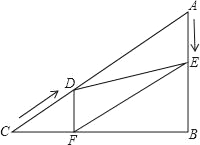
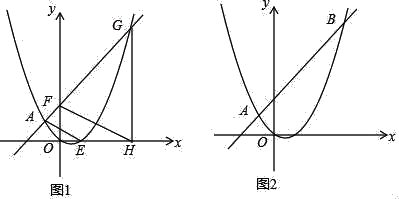
(2)��ͼ1����F������Ϊ��0��m����m��2����ֱ��AF������������һ��G������G��x��Ĵ��ߣ�����ΪH������������x��������ύ�ڵ�E������FH��AE����֤��FH��AE��
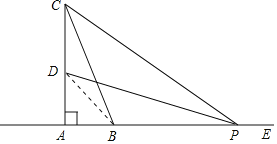
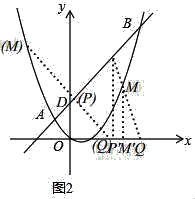
(3)��ͼ2��ֱ��AB�ֱ�x�ᡢy����C��D���㣮��P�ӵ�C������������CD���������˶����ٶ�Ϊÿ��![]() ����λ���ȣ�ͬʱ��Q��ԭ��O��������x�������������˶����ٶ�Ϊÿ��1����λ���ȣ���M��ֱ��PQ�������ߵ�һ�����㣬���˶���t��ʱ��QM=2PM��ֱ��д��t��ֵ��
����λ���ȣ�ͬʱ��Q��ԭ��O��������x�������������˶����ٶ�Ϊÿ��1����λ���ȣ���M��ֱ��PQ�������ߵ�һ�����㣬���˶���t��ʱ��QM=2PM��ֱ��д��t��ֵ��
���𰸡�(1)�����ߵĽ���ʽΪy=x2��x��(2)֤����������(3)���˶�ʱ��Ϊ![]() ��
��![]() ��ʱ��QM=2PM��
��ʱ��QM=2PM��
��������
��1����1��A��B���������������y=ax2+bx��ȷ������ʽ��
��2����A��������������AF�Ľ���ʽ���������ߵĽ���ʽ���ɷ����飬���G�����꣬��ͨ��֤�����������ƣ��õ�ͬλ����ȣ���ֱ��ƽ�У�
��3����������.
���⣺��1������A����1��2����B��3��6�������У�
![]() ����ã�
����ã�![]() ��
��
�������ߵĽ���ʽΪy=x2��x��
��2��֤������ֱ��AF�Ľ���ʽΪy=kx+m��
����A����1��2������y=kx+m������k+m=2��
��k=m��2��
��ֱ��AF�Ľ���ʽΪy=��m��2��x+m��
����ֱ��AF�������߽���ʽ�ɷ�������
![]() ����ã�
����ã�![]() ��
��![]() ��
��
���G��������m��m2��m����
��GH��x�ᣬ
���H��������m��0����
�������ߵĽ���ʽΪy=x2��x=x��x��1����
���E��������1��0����
����A��AA���x�ᣬ����Ϊ��A�䣬��ͼ1��ʾ��
�ߵ�A����1��2����
��A�䣨��1��0����
��AE=2��AA��=2��
��![]() =1��
=1��![]() =
=![]() =1��
=1��
��![]() =
= ![]() ��
��
�ߡ�AA��E=��FOH��
���AA��E�ס�FOH��
���AEA��=��FHO��
��FH��AE��
��3����ֱ��AB�Ľ���ʽΪy=k0x+b0��
��A����1��2����B��3��6������y=k0x+b0�У��� ![]() ����ã�
����ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪy=x+3��
���˶�ʱ��Ϊt��ʱ����P������Ϊ��t��3��t������Q������Ϊ��t��0����
����M���߶�PQ��ʱ������P��PP���x���ڵ�P�䣬����M��MM���x���ڵ�M�䣬���PQP��ס�MQM�䣬��ͼ2��ʾ��
��QM=2PM��
��![]() =
=![]() ��
��
��QM��=![]() QP'=2��MM��=
QP'=2��MM��=![]() PP'=
PP'=![]() t��
t��
���M��������t��2��![]() t����
t����
�֡ߵ�M��������y=x2��x�ϣ�
��![]() t=��t��2��2����t��2����
t=��t��2��2����t��2����
��ã�t=![]() ��
��
����M���߶�QP���ӳ�����ʱ��
ͬ���ɵó���M������Ϊ��t��6��2t����
�ߵ�M��������y=x2��x�ϣ�
��2t=��t��6��2����t��6����
��ã�t=![]() ��
��
�������������˶�ʱ����![]() ��
��![]() ʱ��QM=2PM��
ʱ��QM=2PM��

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�