题目内容
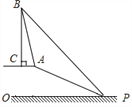
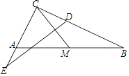
【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB= ![]() ,则DE=________.
,则DE=________.
【答案】![]()
【解析】
设AC=2k,BC=5k,根据勾股定理得到AB=![]() k=20,得到BC=
k=20,得到BC=![]() ,连接DM,根据直角三角形的性质得到AM=CM=BM=
,连接DM,根据直角三角形的性质得到AM=CM=BM=![]() AB=10,由DE是线段CM的垂直平分线,得到CD=DM,根据相似三角形的性质得到CD=
AB=10,由DE是线段CM的垂直平分线,得到CD=DM,根据相似三角形的性质得到CD=![]() ,根据勾股定理得到DN=
,根据勾股定理得到DN=![]() =2,于是得到结论.
=2,于是得到结论.
∵∠C=90°,tanB=![]() ,
,
设AC=2k,BC=5k,
∴AB=![]() k=20,
k=20,
∴k=![]() ,
,
∴BC=![]() ,
,
连接DM,
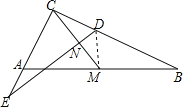
∵∠C=90°,点M是Rt△ABC的斜边AB的中点,
∴AM=CM=BM=![]() AB=10,
AB=10,
∴∠MCB=∠B,
∵DE是线段CM的垂直平分线,
∴CD=DM,
∴∠DCM=∠DMC,
∴△CDM∽△CMB,
∴![]() ,
,
∴CD=![]() ,
,
∵DE垂直平分CM,
∴∠E+∠ECN=∠ECN+∠NCD=90°,
∴∠E=∠NCD,
∴△CDE∽△NDC,
∴![]() ,
,
∵DN=![]() =2,
=2,
∴DE=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目