Question

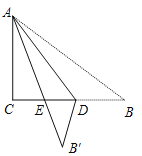
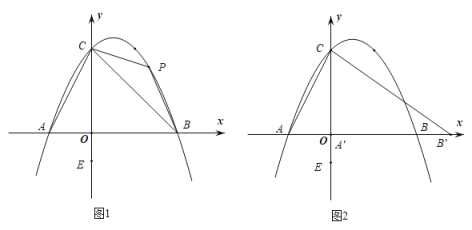
【题目】如图，在平面直角坐标系中，抛物线与轴交于、两点，交轴于点，点关于抛物线对称轴的对称点为点.

（1）求线段的长度；

（2）为线段上方抛物线上的任意一点，点为，一动点从点出发运动到轴上的点，再沿轴运动到点.当四边形的面积最大时，求的最小值；

（3）将线段沿轴向右平移，设平移后的线段为，直至平行于轴（点为第2小问中符合题意的点），连接直线.将绕着旋转，设旋转后、的对应点分别为、，在旋转过程中直线与轴交于点，与线段交于点.当是以为腰的等腰三角形时，写出的长度.

Answer 1

【答案】（1）；（2）3+；（3）CM=或3或2-或2+.

【解析】

（1）先利用函数解析式求得A，B，C的坐标，然后利用两点的距离公式求解即可；

（2）过P作PF平行y轴与BC交于F点，因为△ABC的面积为定值，所以当△PBC的面积最大时，四边形ABPC的面积就最大，直线BC的解析式为y=﹣x+2，设P（a，），F（a,﹣a+2），根据三角形的面积公式得到关于a的一元二次方程，求得当a=时，四边形ABPC的面积最大，此时点P为（，2）；过E作直线l与y轴正方向的夹角为45°，过P作直线l的垂线，垂足为H，与y轴的交点即为符合题意的G点，PG+GE的最小值即为线段PH的长度，然后求出PH的长度即可；

（3）如图2，图3，过O作OK⊥AC交AC于K点，以O为圆心，OK为半径画圆，直线A′C′在旋转过程中始终与☉O相切，由OA·OC=AC·OK得r=OK=，要使△CMN为等腰三角形（MN为腰），分两种情况进行讨论计算即可.

解：（1）令x=0，则y=2，

令y=0，则=0，

解得：x=﹣，或x=2，

∴A（﹣，0），B（2，0），C（0,2），

∴AC=；

（2）如图，过P作PF平行y轴与BC交于F点，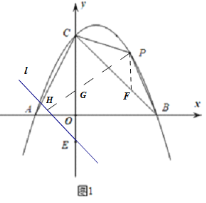

因为△ABC的面积为定值，所以当△PBC的面积最大时，四边形ABPC的面积就最大，

直线BC的解析式为y=﹣x+2，

设P（a，），F（a,﹣a+2），

∴PF=﹣+2a，

则S△PBC=PF·(2﹣0)=﹣a2+2a，

∴当a=时，四边形ABPC的面积最大，

此时，点P为（，2），

过E作直线l与y轴正方向的夹角为45°，过P作直线l的垂线，垂足为H，

与y轴的交点即为符合题意的G点，PG+GE的最小值即为线段PH的长度，

直线l的解析式为：y=﹣x﹣1，

则直线lPH:y=x+，即点G为（0，），

故PG+GE的最小值为；

（3）CM=或3或2-或2+.

过O作OK⊥AC交AC于K点，以O为圆心，OK为半径画圆，直线A′C′在旋转过程中始终与☉O相切，由OA·OC=AC·OK得r=OK=，要使△CMN为等腰三角形（MN为腰），分两种情况：

①如图2，当以∠N为顶角，NC=NM，

∵∠1=∠2，

∴tan∠1=tan∠2=2，

在Rt△OK1M1中，OK1=r=，

∴OM1=，即CM1=；

同理，∠1=∠3，OM2=，即CM2=3；

②如图3，以∠M为顶角，MC=MN，

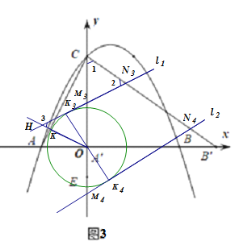
∵∠1=∠3，

∴tan∠1=tan∠3=2，

在Rt△OHK3中，OK3=r=，则HK3=，

在Rt△OK3M3中，设OM3=x，则K3M3=x﹣，

∴（x﹣）2+（）2=x2，

解得：x=，

∴CM3=2﹣；

同理可得，OM4=OM3=,

∴CM4=2+.