题目内容
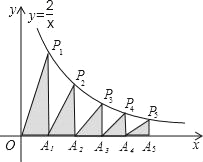
【题目】如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=![]() (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S10=_____.(n≥1的整数)
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S10=_____.(n≥1的整数)
【答案】![]()
【解析】
根据反比例函数y=![]() 中k的几何意义再结合图象即可解答.
中k的几何意义再结合图象即可解答.
因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,S=![]() |k|=1,又因为OA1=A1A2=A2A3=A3A4=A4A5,所以S1=
|k|=1,又因为OA1=A1A2=A2A3=A3A4=A4A5,所以S1=![]() |k|,S2=
|k|,S2=![]() |k|,S3=
|k|,S3=![]() |k|,S4=
|k|,S4=![]() |k|,S5=
|k|,S5=![]() |k|…
|k|…
依此类推:Sn的值为![]() ,
,
当n=10时,S10=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.